|
Question 39858: My friend and I are trying to see who has the right answer to some problems. Could you please explain to us how to solve them the right way.
a. The monthly revenue achieved by selling x boxes of candy is calculated to be $ x(5-0.05x). The wholesale cost of each box of candy is $1.50.
How many boxes must be sold each month to maximize profit?
What is the maximum profit?
(Revenue=Cost+Profit)
b. Bob has 3000ft of fencing available to enclose a rectangular field.
1. Express the area A of rectangle as a function of x where x is the length of rectangle.
2. For what value of x is the area largest?
3.What is the maximum area?
Thank you so much! Now we will see who is right:)
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. The total profit by selling 'x' boxes of candies is
P = $(x(5-0.05x) - 1.5x) = $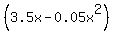
For maximizing 'P',  and and 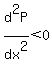
Now, 
or x = 35
and 
Thus P is maximum for x = 35 and corresponding P = $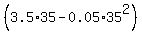 = $61.25. = $61.25.
So for maximum profit, 35 boxes are to be sold and the maximum profit is $61.25.
2. Perimeter = 3000 ft.
Let length = L ft, width = W ft of the rectangular field.
Then, 2(L + W) = 3000 or L + W = 1500 _________(1)
Given: L = x, then from (1) W = 1500 - x.
Hence, area A =  sq ft sq ft
To find maximum area, maximize A w.r.t x as done in the problem above.
Then you get, x = 750 for maximum A and this maximum value of A is 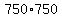 = 562500 = 562500
Hence area of the rectangular field is maximum when its each side is 750 ft i.e. the field is a square with side 750 ft and this maximum area enclosed is 562500 sq ft.
[V.V.I.: From this problem we come to the conclusion that of all rectangles with same perimeter, the square has the largest area.]
|
|
|
| |