Question 398436: 3 children are pythagorean triple at ages 6, 8, and 10. Will they be pythagorean triples again? Show the formula that gave you that answer
Found 2 solutions by MathLover1, richard1234:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
Pythagorean triples are sets of three integers (a, b, and c) which satisfy the equation  .
There are 16 primitive Pythagorean triples with c ≤ 100:
( 3, 4, 5)
( 5, 12, 13)
( 7, 24, 25)
( 8, 15, 17)
( 9, 40, 41)
(11, 60, 61)
(12, 35, 37)
(13, 84, 85)
(16, 63, 65)
(20, 21, 29)
(28, 45, 53)
(33, 56, 65)
(36, 77, 85)
(39, 80, 89)
(48, 55, 73)
(65, 72, 97)
For example, (3, 4, 5) can be doubled to produce (6, 8, 10), which is a Pythagorean triple
and (6, 8, 10) can be doubled to produce (12, 16, 20) which is a Pythagorean triple too
It is possible to devise a formula for producing Pythagorean triples:
if you choose arbitrary positive integers 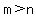 , that these equations generate all Pythagorean Triples (x, y, z):
 ,
 ,
example:
let m=2 and n=1
 ,
 ,
we got first triple from the list above- (3,4,5)
let m=29 and n=25
 ,
 ,
 ...we got second triple (216,1450,1466)
check:
Answer by richard1234(7193)  (Show Source):
|
|
|
