SOLUTION: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC. A. Show that triangle ABC is an isosceles triangle B. Find the coordinates of D , the midpoint of the base

Algebra ->  Geometry-proofs -> SOLUTION: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC. A. Show that triangle ABC is an isosceles triangle B. Find the coordinates of D , the midpoint of the base      Log On


   

Question 397907: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC.
A. Show that triangle ABC is an isosceles triangle
B. Find the coordinates of D , the midpoint of the base.
C. Show that CD is perpendicular to AB
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi, previously posted.

 

A. Show that triangle ABC is an isosceles triangle

B(4,8) and C(6,2)                       A(0,0) and C(6,2)

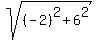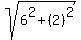
distance AB = sqrt%28+%28-2%29%5E2+%2B+6%5E2%29= distance AC = sqrt%286%5E2+%2B%282%29%5E2+%29



B. Find the coordinates of D , the midpoint of the base AB

A(0,0) and B(4,8)

Midpoint(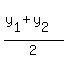%28x%5B1%5D+%2B+x%5B2%5D%29%2F2, %28y%5B1%5D+%2B+y%5B2%5D%29%2F2) (4/2,8/2) OR PT(2,4)



C. Show that CD is perpendicular to AB

 m of CD = %284-2%29+%2F%28+2-6%29+=+2%2F-4+=+-1%2F2

 m of AB = 8/4 = 2

 SLOPES negative reciprocals, lines perpendicular