SOLUTION: Find the intersection of the line through the points (7,10) and (4,2) with the line y=x. The point of intersection is (A,B) where A=? and B=?

Algebra ->  Functions -> SOLUTION: Find the intersection of the line through the points (7,10) and (4,2) with the line y=x. The point of intersection is (A,B) where A=? and B=?      Log On


   

Question 397332: Find the intersection of the line through the points (7,10) and (4,2) with the line y=x. The point of intersection is (A,B) where A=? and B=?
Found 2 solutions by ewatrrr, MathLover1:
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

Using the point-slope formula, m+=%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29 to find slope

(7,10) and 

 (4,2) m = 8/3, the slope of the line containg these points

Using the standard slope-intercept form for an equation of a line y = mx + b

  where m is the slope and b the y-intercept.  

 y = (8/3)x + b  |using ordered pair Pt(4,2) to solve for b

 2 = 32/3 + b

 -26/3 = b

 y = (8/3)x -20/3

 Pt(5,5) is the point of intersection of these lines according to the graph

CHECKING our Answer: 

x = (8/3)x -20/3, 3x = 8x - 20, 20 = 5x, x = 5 and y = 5  (y = x)

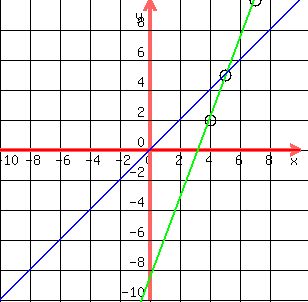
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
given:
x1=+7
+y1=+10
+x2=+4+
y2=+2
solpe m=+%28y2-y1%29%2F%28x2-x1%29
= %282-%2810%29%29%2F%284-%287%29%29
= %282-10%29%2F%284-7%29
= -8%2F-3
=8%2F3

b+=+%28y1-m%2Ax1%29

b+=10-%28%28-8%29%2F%28-3%29%29%287%29+=+10-+%2856%2F3%29+=+-26%2F3
Equation: y=+mx+%2Bb+, m+=+slope
Equation of the line is :

y+=+%288%2F3%29+x+-26%2F3 ----(1)


To find the intersection of this line with y=x, replace+y with x in (1)
x+=+%288%2F3%29x+-+26%2F3

3x=8x-26

-5x=-26

x=26%2F5

y=%288%2F3%29%2826%2F5%29-26%2F3

y=208%2F15+-26%2F3

y=78%2F15+=+26%2F5=5%281%2F5%29

A=5%281%2F5%29

B=5%281%2F5%29

graph:
in standard form you have:
%288%2F3%29+x+-+y+=+26%2F3+
y=x...or x-y=0

Solved by pluggable solver: Solve the System of Equations by Graphing


Let's look at the first equation %288%2F3%29x-y=26%2F3



3%28%288%2F3%29x-y%29=3%2826%2F3%29 Multiply both sides of the first equation by the LCD 3



8x-3y=26 Distribute



---------




So our new system of equations is:


8x-3y=26

1x-y=0





In order to graph these equations, we need to solve for y for each equation.




So let's solve for y on the first equation


8x-3y=26 Start with the given equation



-3y=26-8x Subtract 8+x from both sides



-3y=-8x%2B26 Rearrange the equation



y=%28-8x%2B26%29%2F%28-3%29 Divide both sides by -3



y=%28-8%2F-3%29x%2B%2826%29%2F%28-3%29 Break up the fraction



y=%288%2F3%29x-26%2F3 Reduce



Now lets graph y=%288%2F3%29x-26%2F3 (note: if you need help with graphing, check out this solver)



+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+%288%2F3%29x-26%2F3%29+ Graph of y=%288%2F3%29x-26%2F3




So let's solve for y on the second equation


1x-y=0 Start with the given equation



-y=0-x Subtract +x from both sides



-y=-x%2B0 Rearrange the equation



y=%28-x%2B0%29%2F%28-1%29 Divide both sides by -1



y=%28-1%2F-1%29x%2B%280%29%2F%28-1%29 Break up the fraction



y=x%2B0 Reduce





Now lets add the graph of y=x%2B0 to our first plot to get:


+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C+%288%2F3%29x-26%2F3%2Cx%2B0%29+ Graph of y=%288%2F3%29x-26%2F3(red) and y=x%2B0(green)


From the graph, we can see that the two lines intersect at the point (26%2F5,26%2F5) (note: you might have to adjust the window to see the intersection)