SOLUTION: Hi, I have a big test on complex numbers tomorrow and I am having a very hard time with this particular question: Directions: On a complex plane, a point z has been graphed. you

The other tutor messed up, although he's right about the 2nd quadrant
between  and .



Here is the point:


    
We draw a line from the origin to the point.  The length of that line is
indicated by the letter "r"



Now we indicate θ with a red arc that starts on the right
side of the x-axis and swings counter-clockwise to the green
line:



Next we draw a perpendicular from the point to the x-axis. The blue
line below, which we label as y.



Now we have a right triangle, with the horizontal leg labeled as x,


Since we are given = cos(θ) = 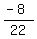 and we know that
cos(θ) = , we will take x to be -8 and r to be 22,
So we label those:



Now we calculate y by the Pythagorean theorem:

     r² = x² + y²

  (22)² = (-8)² + y²

    484 = 64 + y²

    420 = y²
    ___
   ⎷420 = y
  _____
 ⎷4*105 = y
    ___
  2⎷105 = y

So we label y:


                                                                 ___
Therefore the given point, call it P has the coordinates P(-8, 2⎷105).


                                                ___
Therefore z in standard form is x + yi = -8 + 2⎷105*i 

z in trigonometric form is r(cosθ + isinθ)

But we must find θ by using the given cosθ =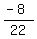 

We use the inverse cosine of the POSITIVE  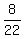to find the
reference angle of θ to be 68.7° or as a whole number of degrees,
69°.  But to get that in the second quadrant we subtract from 180°
and get θ = 111°

Now the trig form

r(cosθ + isinθ)

becomes 
  ___
2⎷105(cos111° + i*sin111°)

Edwin