Question 395583: Could you please help me? I'm not sure how to answer the following question because I don't understand how to 'calculate' the answer:
Q. Calculate the following, giving your answers in the form p/q, where p,q = Z
log(base4)(64) , log(base8)(64), log(base32)(64)
log(base7)(49) , log(base49)(49) , log(base343)(49)
log(base1/5)(125) , log(base1/125)(125) , log(base1/625)(125)
log(base8)(512) , log(base2)(512) , log(base16)(512)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! These are too many questions to post all at once. I will help with some of them in hopes that you will then know how to do the rest on your own.
First, let's be clear about what a logarithm is. Logarithms are exponents. The idea behind logarithms is that you can take any positive number (other than 1) and obtain any other positive number if you raise it to the correct power. For example, if you raise 3 to the correct power you can get a 4! This exponent is expressed as  . In general . In general 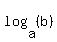 represents the exponent to use on "a" to get a "b". represents the exponent to use on "a" to get a "b".
Once we get what a logarithm represents, some of your problems are extremely easy:
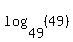 represents the exponent for 49 that results in 49. What power of 49 is 49? Answer: 1! (Or 1/1) represents the exponent for 49 that results in 49. What power of 49 is 49? Answer: 1! (Or 1/1)
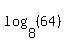 represents the exponent for 8 that results in 64. If you know your multiplication facts you know the answer is 2 (or 2/1). represents the exponent for 8 that results in 64. If you know your multiplication facts you know the answer is 2 (or 2/1).
 represents the exponent for 1/125 that results in 125. If you know about negative exponents you will see that the exponent that turns 1/125 into 125 is -1! (-1/1) represents the exponent for 1/125 that results in 125. If you know about negative exponents you will see that the exponent that turns 1/125 into 125 is -1! (-1/1)
Some you have to work at a little:
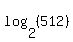 represents the exponent for 2 that results in 512. With the help of a calculator (or calculator computer program) and a little trial and error, you will find that 2 to the 9th power is 512. represents the exponent for 2 that results in 512. With the help of a calculator (or calculator computer program) and a little trial and error, you will find that 2 to the 9th power is 512.
And some are even harder:
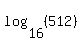 represents the exponent for 16 that results in 512. But try as you might, you cannot find the right exponent. 512 is not a whole number power of 16. With these problems look to see if both the base and the argument are powers of some third number. In this case both the base, 16, and the argument, 512, are powers of 2! represents the exponent for 16 that results in 512. But try as you might, you cannot find the right exponent. 512 is not a whole number power of 16. With these problems look to see if both the base and the argument are powers of some third number. In this case both the base, 16, and the argument, 512, are powers of 2!  and and  . When this happens you use the base conversion formula, . When this happens you use the base conversion formula,  , to change the base: , to change the base:
 So So  ! !
All of your other problems can be done in one of these ways:- Just know what the right exponent is
- Trying different exponents on the base until you find the right one.
- If neither of the two above work, then see if both the base and argument are powers of the same third number. If they are then use the base conversion formula.
Final note: While all you problems can be done this way. Some logarithms cannot. The earlier example I gave you,  cannot be found in any of these ways. This logarithm (and others like it) cannot be expressed as a rational number. cannot be found in any of these ways. This logarithm (and others like it) cannot be expressed as a rational number.
|
|
|