Question 394889: Prove: The probability that two diagonals in a convex polygon with n sides will intersect inside the polygon is 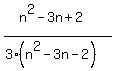 . .
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! The condition of convexity ensures that any diagonal will be in the interior of the polygon (except for the endpoints of course, which correspond to vertices.)
For any given n-gon, the number of diagonals that can be formed is  . Hence the total number of diagonal pairs that can be formed is . Hence the total number of diagonal pairs that can be formed is  . .
Now to find the total number of diagonal pairs that intersect inside the polygon, we only have to count the total number of quadrilaterals that we can form from the vertices of the n-gon, i.e.,  . .
The reason for this is that, a quadrilateral always has a unique pair of diagonals intersecting inside it, and so the number of quadrilaterals is the same as the number of pairs of diagonals meeting inside the convex n-gon.
Hence the probability is 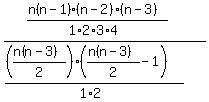
=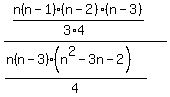
= , after simplification. , after simplification.
Note that this formula will work only for positive integers  . For the triangle (n = 3), this formula won't make sense (the formula will give probability -1/3, which is absurd). For the triangle the probability is 0( because no quadrilateral can be formed.) . For the triangle (n = 3), this formula won't make sense (the formula will give probability -1/3, which is absurd). For the triangle the probability is 0( because no quadrilateral can be formed.)
|
|
|