SOLUTION: Prove: The probability that two diagonals in a convex polygon will intersect inside the polygon is {{{(n^2 - 3n + 2)/(3(n^2 -3n -2))}}}.

Algebra ->  Formulas -> SOLUTION: Prove: The probability that two diagonals in a convex polygon will intersect inside the polygon is {{{(n^2 - 3n + 2)/(3(n^2 -3n -2))}}}.      Log On


   

Question 394879: Prove: The probability that two diagonals in a convex polygon will intersect inside the polygon is 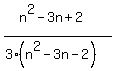%28n%5E2+-+3n+%2B+2%29%2F%283%28n%5E2++-3n++-2%29%29.
Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
Sorry, I had misread the minus as a plus and nearly thought that the probability was 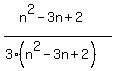%28n%5E2+-+3n+%2B+2%29%2F%283%28n%5E2++-3n++%2B2%29%29 which simplifies to 1/3 (and doesn't make sense). I have revised my solution here, but didn't have enough time to finish, as there is probably going to be a ton of algebra. However I have got you started, you can finish the algebra from then on.



I'm quite sure that the best way is to fix one of the n points a%5B1%5D, a%5B2%5D, ..., a%5Bn%5D at a%5B1%5D. We go case by case on what the second point of diagonal D%5B1%5D is.

Case 1: D%5B1%5D includes points a%5B1%5D and a%5B3%5D.

Then, there is 1 point between a%5B1%5D and a%5B3%5D and n-3 points from a%5B3%5D to a%5B1%5D (counting all the numbers 4, 5, ..., n inclusive).

We can generalize this to say:

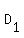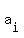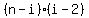If D%5B1%5D comprises of points a%5B1%5D, a%5Bi%5D, then there are %28n-i%29%28i-2%29 possible diagonals. Given this, we can sum them up from i = 3 to i = n-1. If P is the total number of diagonals, then

(subtracting the case where n = 1, 2)

After this, use the sum identities sum%28i%5E2%2C+i+=+1%2C+k%29+=+k%28k%2B1%29%282k%2B1%29%2F6 and sum%28i%2C+i+=+1%2C+k%29+=+k%28k%2B1%29%2F2. After that, it's pretty much algebra bashing time to find an expression for P.

Suppose Q is the number of sets of two diagonals. Be careful that one of the diagonals of Q must have an endpoint at a%5B1%5D (due to our previous assumption).

The probability that two chosen diagonals intersect is then P/Q, which should turn out to the expected value (however it's a whole lot of algebra and simplifying from here on).




The other solution I considered involved mathematical induction. Basically, you show the base case (n=4, trivial), and show that n = k implies n = k+1. However, I had to split this problem into two cases, one case where the diagonals in the (n+1)-gon were contained within the n-gon, and the other case where one diagonal contains the (n+1)th point. However this solution is probably a bit longer than this one.