SOLUTION: Prove the identity: {{{Sec(x)-Tan(x)Sin(x)=1/(Sec(x))}}}

The other tutor multiplied both sides by a factor which
is not allowed in proving identities because it amounts
to assuming what you are to prove, that is, that the equal
sign holds. You must only work with one side, and never do 
something to both sides, since you don't know the equal 
sign holds until you've proved it is one.  Here's the
correct way to prove it:

Prove the identity:















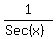Edwin