|
Question 392999: when a three digit number is divided by the sum of the digits of the number, the quotient is 26. What is the least number for which this is true?
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! We have
 --> -->  (a, b, c are digits). Subtracting (a, b, c are digits). Subtracting 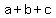 from both sides, from both sides,

This implies 9 divides a+b+c and 25 divides 11a+b. Therefore, the only possible values of a+b+c are 9, 18, 27 (since 36 is too high).
Suppose a+b+c = 9. Then,  , and , and  (by substituting) which is divisible by 25. Since 9 - c + 10a is congruent to 9 - c (mod 10) = 5 or 0, the only possibility for c is 4 (since 9 is impossible). This leaves (by substituting) which is divisible by 25. Since 9 - c + 10a is congruent to 9 - c (mod 10) = 5 or 0, the only possibility for c is 4 (since 9 is impossible). This leaves  (note that 11a + b is divisible by 25). The easiest way is simply guess and check to find any solutions; we see that a = 2, b = 3 works since 11(2) + 3 is divisible by 25. (note that 11a + b is divisible by 25). The easiest way is simply guess and check to find any solutions; we see that a = 2, b = 3 works since 11(2) + 3 is divisible by 25.
Therefore the smallest number is 234.
|
|
|
| |