Question 392725: I am not positive that this is a Trigonometry problem, but I have looked through all of the other subjects and I do not know which one it would fit under, I was thinking maybe something with geometry but I am not sure. If you cannot help me with this problem, I understand. If you know what category it fits under and could let me know, that would be great! This is the problem I am stuck on: A trapezoid with bases 12 and 20 is inscribed in a semi-circle. Find the length of each leg.
I have looked at it for a while and just cannot seem to get anywhere. I know you will probably have to draw a diagonal to find the answers but you do not know any angle measurements or anything else about the semi-circle or trapezoid so I do not even know where to begin. Any help would be greatly appreciated and I thank you so much! If it helps at all, I am in a 10th grade honors class. Thanks again(:
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source):
Answer by Edwin McCravy(20064)  (Show Source):
You can put this solution on YOUR website!
Oh, yes, there is enough information.
Let O be the center of the semicircle. BC, which is 20 units long
is a diameter of the semicircle, so OB is a radius and is 10 unit
long.
Draw radius OA, which is also 10 units long.
Draw OE perpendicular to both bases of the trapezoid, splitting the
upper 12-unit base AD of the trapezoid into two segments AE and DE,
each 6 units long.
Triangle AEO is a right triangle and we can use the
Pythagorean theorem to find OE.
So we label OE as 8 units long.
Draw AF parallel and equal in length to OE, which
is also 8 units long:
Since AE is the same length as OF, OF is also 6 units long,
and since OB is 10 units long, BF is 10-6 or 4 units long:
Now since ABF is a right triangle, we can find AB using the
Pythagorean theorm:
And CD is also 
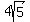or about 8.94427191 units long
Edwin
|
|
|
