Question 392072: A collection of 90 coins, pennies, nickels, and dimes, has a value of $2.85. If there are twice as may pennies as there are nickels and dimes combined, how many pennies, dimes, and nickels are there?
Found 2 solutions by ankor@dixie-net.com, mananth:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A collection of 90 coins, pennies, nickels, and dimes, has a value of $2.85.
If there are twice as may pennies as there are nickels and dimes combined, how many pennies, dimes, and nickels are there?
:
p + n + d = 90
:
.01p + .05n + .10d = 2.85
:
"there are twice as may pennies as there are nickels and dimes combined,"
p = 2(n + d)
divide both sides by 2
.5p = n + d
.5p - n - d = 0; add to the 1st equation
p + n + d = 90
----------------------eliminates n and d find p
1.5p = 90
p = 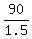
p = 60 pennies
:
Rewrite the two equation using p=60
n + d = 30
n = (30-d)
and
.05n + .10d = 2.25
Substitute (30-d) for n
.05(30-d) + .10d = 2.25
1.5 - .05d + .10d = 2.25
.05d = 2.25 - 1.50
d = 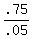
d = 15 dimes
then obviously
n = 15 nickels
:
:
Check solutions by finding the total$
.01(60) + .05(15) + .10(15) =
.60 + .75 + 1.5 = 2.85, confirms our solution p=60; n=15; d=15
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! A collection of 90 coins, pennies, nickels, and dimes, has a value of $2.85. If there are twice as may pennies as there are nickels and dimes combined, how many pennies, dimes, and nickels are there?
..
x nickels
y dimes
z pennies
..
z= 2(x+y)...................1
x+y+z=90.....................2
5x+10y+z=285.................3
..
plug z in (2) & (3)
x+y+2(x+y) = 90
(x+y+x+y)= 90
3x+3y=90
/3
x+y = 30,,,,,,,,,,,,,,4
...
5x+10y+z= 285
5x+10y +2(x+y) = 285
7x+12y=285,,,,,,,,,,,,,5
...
multiply (4) by -7
we get
-7x-7y=-210
add to (5)
5y=75
y=15 dimes
from (4) x+y =30
x+15=30
x= 15 nickels
balance 15 are pennies
60 pennies, 15 dimes,15 nickels
...
CHECK
60+150+75=285
...
m.ananth@hotmail.ca
...
|
|
|