SOLUTION: Find the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus-rectum.

Algebra ->  Test -> SOLUTION: Find the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus-rectum.      Log On


   

Question 391957: Find the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus-rectum.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

Note: the vertex form of a parabola, y=a%28x-h%29%5E2+%2Bk where(h,k) is the vertex

Parabola: x^2 = 12y  OR 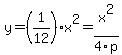y+=+%281%2F12%29x%5E2++=+x%5E2%2F4p where Pt(0,p) is the focus 

parabola with center at Pt(0,0) and Pt(0,3) is the focus

and the length of the latus rectum chord = 4p = 12

the area of the triangle formed joining (Pt(0,0) to the ends of its latus-rectum

A = (1/2)b*h = 1/2 * 12 * 3 = 18