Question 391550: How do you find the vertical and horizontal asymptotes of a function?
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! A vertical asymptote occurs when there exists an x such that f(x) = p/0, where p is nonzero. For example, the function  has a vertical asymptote at x = 3, since you obtain f(3) = 8/0, but the function  does not have a vertical asymptote at -2, since the function is equivalent to  except at -2 (where a "gap" in the function exists). Also, substituting x = -2, we get 0/0 which is indeterminate.
On the other hand, a horizontal asymptote occurs when a function converges to a limit as x goes to infinity or negative infinity. In limit notation, a function has a horizontal asymptote if 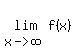 exists (or if the limit as x approaches negative infinity exists). There are many types of functions with horizontal asymptotes, and many different ways to find them.
|
|
|
