Question 391158: what is the maximum area of a rectangle with a perimeter of 100 feet
Found 2 solutions by Alan3354, richard1234:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Many different ways to solve this.
Solution 1
----------
If the sides of the rectangle are x and 50-x (so that the perimeter is 100), the area is  , which is a parabola in terms of x. The vertex occurs at , which is a parabola in terms of x. The vertex occurs at 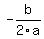 , or x = 25. It points downward, so x = 25 maximizes the area, so the area is 625. , or x = 25. It points downward, so x = 25 maximizes the area, so the area is 625.
Solution 2
----------
Another way is finding the extrema of  . We have . We have  which is equal to zero when x = 25 (this is actually where the -b/2a rule comes from). which is equal to zero when x = 25 (this is actually where the -b/2a rule comes from).
Solution 3
----------
Yet another way comes from an unusual theorem: AM-GM inequality. Suppose we have two terms  and and  . Then by AM-GM, . Then by AM-GM,
 Since Since  , ,  , ,


The AM-GM inequality says the equality occurs if and only if all the 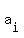 's are equal, that is, 's are equal, that is,  , and the optimal area is 625. , and the optimal area is 625.
It's pretty rare you'll see a solution like the last one. However AM-GM can be used to prove many similar theorems, i.e. proving that the rectangular solid of fixed surface area that has maximum volume is a cube.
|
|
|