SOLUTION: if a,b,c are in continued proportion, prove that: (a^2+b^2+c^3)/(a+b+c)=a-b+c and hence find three numbers in continued proportion so that their sum is 14 and the sum of their

Algebra ->  Proportions -> SOLUTION: if a,b,c are in continued proportion, prove that: (a^2+b^2+c^3)/(a+b+c)=a-b+c and hence find three numbers in continued proportion so that their sum is 14 and the sum of their       Log On


   

Question 390900: if a,b,c are in continued proportion, prove that:
(a^2+b^2+c^3)/(a+b+c)=a-b+c
and hence find three numbers in continued proportion so that their sum is 14 and the sum of their squares is 84
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
You definitely mean %28a%5E2%2Bb%5E2%2Bc%5E2%29%2F%28a%2Bb%2Bc%29=a-b%2Bc.
The given is a%2Fb+=+b%2Fc, that is, a,b,c are in continued proportion . One consequence of this condition is the fact that ac+=+b%5E2, which we will use later.
To start off, consider 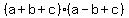%28a%2Bb%2Bc%29%28a-b+%2B+c%29. Upon expansion, this is equal to .
But ac+=+b%5E2, so after substitution,
%28a%2Bb%2Bc%29%28a+-b+%2B+c%29+=+a%5E2+%2B+b%5E2+%2B+c%5E2. Assuming that the sum a+b+c is not equal to zero, then we divide by a+b+c, and the result follows.
Consider a = 8, b = 4, and c = 2. Then %2864%2B16+%2B+4%29%2F%288%2B4%2B2%29+=+6.