Question 390785: Make up a polynomial that meets the following conditions:
a)it has rational zeros 3/4 and -1/3
b)it has two complex roots of the form a+bi,a,b "not equal" to 0
Then, create the list of all possible rational roots and use synthetic division to reduce the 4th degree polynomial to a quadratic and solve for the remaining roots. Show all steps.
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! There's an important theorem called "The Fundamental Theorem of Algebra" (it looks easy, but requires high-level analysis to prove) that says that any n-degree polynomial has n roots, counting multiplicities.
Furthermore, if r is a root of the polynomial, then (x-r) is a factor of it (this will be useful in generating the polynomial).
Therefore the polynomial P(x) is equal to
You write in your problem "Then, create the list of all possible rational roots and use synthetic division to reduce the 4th degree polynomial to a quadratic and solve for the remaining roots. Show all steps." However, the only rational roots are 3/4 and -1/3. The quadratic with a double root x - a - bi has double root 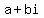 . Therefore, solving for the remaining roots using synthetic division is unnecessary...only do that if you're practicing your synthetic division :)
|
|
|
