SOLUTION: can you help me solve this: In a system of axes consider the points A(-1,0) B(2,0) and M(x,y) such that x^2-x-2+y^2=0 how can i find M ??

Algebra ->  Coordinate-system -> SOLUTION: can you help me solve this: In a system of axes consider the points A(-1,0) B(2,0) and M(x,y) such that x^2-x-2+y^2=0 how can i find M ??      Log On


   

Question 390232: can you help me solve this:
In a system of axes consider the points A(-1,0) B(2,0) and M(x,y)
such that x^2-x-2+y^2=0
how can i find M ??
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
can you help me solve this:
In a system of axes consider the points A(-1,0) B(2,0) and M(x,y)
such that x²-x-2+y²=0
Here are those points plotted:

how can i find M ??
x² - x - 2 + y² = 0

x² - x + y² = 2

x² - x + 1%2F4 + y² = 2 + 1%2F4

(x - 1%2F2)² + (y - 0)² = 9%2F4

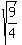So this is a circle with center (h,k) = (1%2F2, 0) and r = sqrt%289%2F4%29 = 3%2F2 

We draw that circle:



M(x,y) is any point on that green circle, including the two given points.

There are an infinite number of solutions because there are an infinite 
number of points on the circle.

Here are 4 possible solutions for M(x,y)

M(0,sqrt%282%29)

M(0,-sqrt%282%29)

M(1,sqrt%282%29)

M(1,-sqrt%282%29)
 
They are all on the circle.  I'll plot them in red:



But realize that there are infinitely many solutions for M(x,y) since there
are infinitely many points on the green circle besides those 4 plotted
in red above.

Edwin