SOLUTION: 5^log25(4x)=4^2

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: 5^log25(4x)=4^2      Log On


   

Question 389999: 5^log25(4x)=4^2
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
5%5Elog%2825%2C+%284x%29%29=4%5E2
I'll solve this two ways. The first method depends on knowing
  • a%5Elog%28a%2C+%28q%29%29+=+q for any valid "a" and any valid "q"
  • 25, the base of the logarithm, is a power of 5 and vice versa.

The second way is more straightforward but more involved.

Method 1: Since 25+=+5%5E2, 5+=+25%5E%281%2F2%29 Replacing the 5 we get:
%2825%5E%281%2F2%29%29%5Elog%2825%2C+%284x%29%29=4%5E2
The rule for exponents when raising a power to a power is to multiply so this becomes:
25%5E%28%281%2F2%29log%2825%2C+%284x%29%29%29=4%5E2
Now we can use a property of logarithms, q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29, to move the 1/2 from in front into the argument as an exponent:
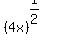25%5Elog%2825%2C+%28%284x%29%5E%281%2F2%29%29%29=4%5E2
We now have the a%5Elog%28a%2C+%28q%29%29+=+q form with "a" being 25 and "q" being %284x%29%5E%281%2F2%29. So this simplifies to:
%284x%29%5E%281%2F2%29+=+4%5E2
Now we can solve for x. Squaring both sides we get:
4x = 256
Dividing by 4 we get:
x = 64

Method 2: The "normal" approach to solving an equation where the variable is in an exponent is to start by writing the equation in logarithmic form. The base of logarithm to use is not significantly important. But if we use the base of the exponent, 5, we will end up with a simpler expression. So we will use base 5:
log%285%2C+%285%5Elog%2825%2C+%284x%29%29%29%29=log%285%2C+%284%5E2%29%29
Using the q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29 property to move the exponent of the argument out in front we get:
%28log%2825%2C+%284x%29%29%29log%285%2C+%285%29%29=log%285%2C+%284%5E2%29%29
Since log%285%2C+%285%29%29+=+1 by definition, this simplifies to:
log%2825%2C+%284x%29%29=log%285%2C+%2816%29%29
The next step can be several different things. Probably the best is to use the base conversion formula for logarithms, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to convert one of the two logarithms into the same base as the the other. We will convert the base 25 logarithm into an expression of base 5 logarithms:
log%285%2C+%284x%29%29%2Flog%285%2C+%2825%29%29+=+log%285%2C+%2816%29%29
Since 25+=+5%5E2, log%285%2C+%2825%29%29+=+2. So this becomes:
log%285%2C+%284x%29%29%2F2+=+log%285%2C+%2816%29%29
Multiplying both sides by 2 we get:
log%285%2C+%284x%29%29+=+2log%285%2C+%2816%29%29
Next we can use the q%2Alog%28a%2C+%28p%29%29+=+log%28a%2C+%28p%5Eq%29%29 property again to move the 2 from in front, into the argument as an exponent:
log%285%2C+%284x%29%29+=+log%285%2C+%2816%5E2%29%29
or
log%285%2C+%284x%29%29+=+log%285%2C+%28256%29%29
Now the equation says two base 5 logarithms are equal. This must mean that the arguments are equal, too:
4x = 256
Divide by 4 and we get:
x = 64