Question 389682: Prove or disprove: The rectangular solid of minimum surface area with fixed volume is a cube.
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! Without loss of generality, let the fixed volume be 1, and the dimensions of the rectangular solid be x, y, z. Then,
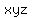 = 1, and we want to show whether
 -->  is true (if it is true, then the solid must have a surface area of at least 6, and the solid of least surface area is a cube).
Applying the AM-GM inequality,
Since  , replace it into the right-hand side and simplify:
as desired. The equality of AM-GM occurs when x = y = z, i.e. the rectangular solid is a cube.
|
|
|
