|
Question 389645: Solving Quadratic Equations by factoring (when first cioefficient is negative).
pls walk me thru each step:
-5x^2 + 2x +3 = 0
i know we multiply by -1 to change each sign:
5x^2 -2x -3. then we factor. but I am being told that the factors are
(5x + 3) (x - 1) = 0. I do not understand this. Why isn't it -3, & +1???
I just don't understand the answer to be x = - 3/5 or x = 1, Seems it should be the opposite.
thank you
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 ........ multiply by ........ multiply by 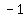 to change each sign to change each sign
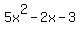
then we factor
| Solved by pluggable solver: Factoring using the AC method (Factor by Grouping) |
Looking at the expression 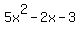 , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is  . .
Now multiply the first coefficient  by the last term by the last term  to get to get  . .
Now the question is: what two whole numbers multiply to  (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of  (the previous product). (the previous product).
Factors of  : :
1,3,5,15
-1,-3,-5,-15
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*(-15) = -15
3*(-5) = -15
(-1)*(15) = -15
(-3)*(5) = -15
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | -15 | 1+(-15)=-14 | | 3 | -5 | 3+(-5)=-2 | | -1 | 15 | -1+15=14 | | -3 | 5 | -3+5=2 |
From the table, we can see that the two numbers  and and  add to add to  (the middle coefficient). (the middle coefficient).
So the two numbers  and and  both multiply to both multiply to  and add to and add to 
Now replace the middle term  with with 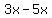 . Remember, . Remember,  and and  add to add to  . So this shows us that . So this shows us that  . .
 Replace the second term Replace the second term  with with 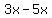 . .
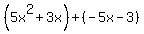 Group the terms into two pairs. Group the terms into two pairs.
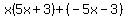 Factor out the GCF Factor out the GCF  from the first group. from the first group.
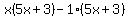 Factor out Factor out  from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis. from the second group. The goal of this step is to make the terms in the second parenthesis equal to the terms in the first parenthesis.
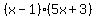 Combine like terms. Or factor out the common term Combine like terms. Or factor out the common term 
===============================================================
Answer:
So 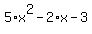 factors to factors to 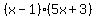 . .
In other words,  . .
Note: you can check the answer by expanding 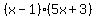 to get to get 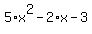 or by graphing the original expression and the answer (the two graphs should be identical). or by graphing the original expression and the answer (the two graphs should be identical).
|
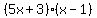 ...set to zero ...set to zero
 ........product is equal to zero if at least one or both factors are equal to zero, so you will have ........product is equal to zero if at least one or both factors are equal to zero, so you will have
 .....-> .....-> .....-> .....-> ....or ....or
 ......-> ......-> ... ...
the answer is:  or or 
another way to check the result:
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=5, b=-2, and c=-3 Plug in a=5, b=-2, and c=-3
 Negate -2 to get 2 Negate -2 to get 2
 Square -2 to get 4 (note: remember when you square -2, you must square the negative as well. This is because Square -2 to get 4 (note: remember when you square -2, you must square the negative as well. This is because  .) .)
 Multiply Multiply  to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 5 to get 10 Multiply 2 and 5 to get 10
So now the expression breaks down into two parts
 or or 
Lets look at the first part:

 Add the terms in the numerator Add the terms in the numerator
 Divide Divide
So one answer is

Now lets look at the second part:

 Subtract the terms in the numerator Subtract the terms in the numerator
 Divide Divide
So another answer is

So our solutions are:
 or or 
|
|
|
|
| |