|
Question 389589: Find the X-intercept of the parabola with vertex (-1,-108) and y-intercept of (0,-105).
Found 2 solutions by ewatrrr, Edwin McCravy:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi,
the vertex form of a parabola,  where(h,k) is the vertex
vertex (-1,-108)
y =a(x+1)^2 -108
using y-intercept pt(0,-105) to find a
-105 = a(1)^2 -108
3 = a
y = 3(x+1)^2 -108
finding x-intercepts when y = 0
0 = 3(x+1)^2 -108
108 = 3(x+1)^2
36 = (x+1)^2
6 = (x+1) x = 5
-6 = (x+1) x -7
x-intercepts are Pt(5,0) and Pt(-7,0)
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website! Find the X-intercept of the parabola with vertex (-1,-108) and y-intercept of (0,-105).
Use the form for the parabola:
y = a(x - h)² + k with vertex (h,k) = (-1,-108)
y = a[x - (-1)]² + (-108)
y = a(x + 1)² - 108
Since y-intercept (0,-105) must satisfy the equation
we substitute 0 for x any -105 for y:
y = a(x + 1)² - 108
-105 = a(0 + 1)² - 108
-105 = a(1)² - 108
-105 = a*1 - 108
-105 = a - 108
3 = a
So we substitute 3 for a in
y = a(x + 1)² - 108
and get
y = 3(x + 1)² - 108
That's the equation of the parabola
To find the x intercept we substitute 0 for y:
0 = 3(x + 1)² - 108
108 = 3(x + 1)²
Divide both side by 3
36 = (x + 1)²
Use the principle of square roots:
__
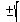 36 = x + 1
±6 = x + 1
Using the +6
6 = x + 1
5 = x
Using the -6
-6 = x + 1
-7 = x
So there are two x-intercepts (5,0) and (-7,0)
Edwin
|
|
|
| |
