Question 389523: Show that the rectangular solid of maximum surface area inscribed in a sphere is a cube.
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! This is actually somewhat similar to a previous solution I posted, in which the question was asking to prove that the rectangular solid of maximum volume inscribed in a sphere was a cube.
Let x, y, z be the dimensions of the rectangular solid, and without loss of generality let the diameter of the sphere be  (I assigned this number in the previous solution as well). From this, we establish that:
 (this follows from Pythagorean theorem)
Surface area =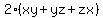 
Such an inscribed cube has side length 1, and has surface area of 6.
We want to prove that
 --> 
To show this, I used the Cauchy-Schwarz inequality (see below) letting a_1 = x, a_2 = y, a_3 = z, b_1 = y, b_2 = z, b_3 = x.
Since  , the left hand side equals 9. Therefore we can substitute 9 and take the square root of both sides to obtain
as desired. Note that the equality case occurs when x = y = z, i.e. the rectangular solid is a cube.
This is probably the easiest solution, there might be other solutions using optimization given a derivative of a function of two variables x,y (since z is determined from x,y). However it would be rather lengthy compared to this solution (it's pretty amazing that the Cauchy-Schwarz inequality produces the result immediately).
Note: the Cauchy-Schwarz inequality says that, for positive real numbers a_1, a_2, ..., a_n and b_1, b_2, ...b_n, then
 The equality case occurs when all a_i are equal to c*(b_i) where c is a constant.
|
|
|
