|
Question 389186: Please show me how to Solve the equation x2 + 8x – 2 = 0 using both The quadratic formula and Completing the square.
Found 2 solutions by haileytucki, jim_thompson5910:
Answer by haileytucki(390)   (Show Source): (Show Source):
You can put this solution on YOUR website! Quadratic First (~=square root)
x^(2)+8x-2=0
Use the quadratic formula to find the solutions. In this case, the values are a=1, b=8, and c=-2.
x=(-b\~(b^(2)-4ac))/(2a) where ax^(2)+bx+c=0
Use the standard form of the equation to find a, b, and c for this quadratic.
a=1, b=8, and c=-2
Substitute in the values of a=1, b=8, and c=-2.
x=(-8\~((8)^(2)-4(1)(-2)))/(2(1))
Simplify the section inside the radical.
x=(-8\6~(2))/(2(1))
Simplify the denominator of the quadratic formula.
x=(-8\6~(2))/(2)
First, solve the + portion of +-.
x=(-8+6~(2))/(2)
Factor out the GCF of 2 from each term in the polynomial.
x=(2(-4)+2(3~(2)))/(2)
Factor out the GCF of 2 from -8+6~(2).
x=(2(-4+3~(2)))/(2)
Reduce the expression (2(-4+3~(2)))/(2) by removing a factor of 2 from the numerator and denominator.
x=(-4+3~(2))
Remove the parentheses around the expression -4+3~(2).
x=-4+3~(2)
Next, solve the - portion of +-.
x=(-8-6~(2))/(2)
Factor out the GCF of 2 from each term in the polynomial.
x=(2(-4)+2(-3~(2)))/(2)
Factor out the GCF of 2 from -8-6~(2).
x=(2(-4-3~(2)))/(2)
Reduce the expression (2(-4-3~(2)))/(2) by removing a factor of 2 from the numerator and denominator.
x=(-4-3~(2))
Remove the parentheses around the expression -4-3~(2).
x=-4-3~(2)
The final answer is the combination of both solutions.
x=-4+3~(2),-4-3~(2)_x=0.2426407,-8.24264
Now, completing the square
x^(2)+8x-2=0
Since -2 does not contain the variable to solve for, move it to the right-hand side of the equation by adding 2 to both sides.
x^(2)+8x=2
To create a trinomial square on the left-hand side of the equation, add a value to both sides of the equation that is equal to the square of half the coefficient of x. In this problem, add (4)^(2) to both sides of the equation.
x^(2)+8x+16=2+16
Add 16 to 2 to get 18.
x^(2)+8x+16=18
Factor the perfect trinomial square into (x+4)^(2).
(x+4)^(2)=18
Take the square root of each side of the equation to setup the solution for x.
~((x+4)^(2))=\~(18)
Remove the perfect root factor (x+4) under the radical to solve for x.
(x+4)=\~(18)
Pull all perfect square roots out from under the radical. In this case, remove the 3 because it is a perfect square.
(x+4)=\3~(2)
First, substitute in the + portion of the \ to find the first solution.
(x+4)=3~(2)
Remove the parentheses around the expression x+4.
x+4=3~(2)
Since 4 does not contain the variable to solve for, move it to the right-hand side of the equation by subtracting 4 from both sides.
x=-4+3~(2)
Move all terms not containing x to the right-hand side of the equation.
x=3~(2)-4
Next, substitute in the - portion of the \ to find the second solution.
(x+4)=-3~(2)
Remove the parentheses around the expression x+4.
x+4=-3~(2)
Since 4 does not contain the variable to solve for, move it to the right-hand side of the equation by subtracting 4 from both sides.
x=-4+-3~(2)
Move all terms not containing x to the right-hand side of the equation.
x=-3~(2)-4
The complete solution is the result of both the + and - portions of the solution.
x=3~(2)-4,-3~(2)-4
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solving by use of the quadratic formula:
 Start with the given equation. Start with the given equation.
Notice that the quadratic 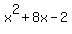 is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "x":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 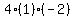 to get to get 
 Rewrite Rewrite 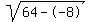 as as 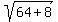
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Simplify the square root (note: If you need help with simplifying square roots, check out this solver) Simplify the square root (note: If you need help with simplifying square roots, check out this solver)
 Break up the fraction. Break up the fraction.
 Reduce. Reduce.
 or or  Break up the expression. Break up the expression.
So the solutions are  or or 
----------------------------------------------------------------------------
Solving by use of completing the square:
First we need to complete the square for the expression 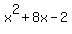
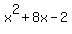 Start with the given expression. Start with the given expression.
Take half of the  coefficient coefficient  to get to get  . In other words, . In other words,  . .
Now square  to get to get  . In other words, . In other words, 
 Now add and subtract Now add and subtract  . Make sure to place this after the "x" term. Notice how . Make sure to place this after the "x" term. Notice how  . So the expression is not changed. . So the expression is not changed.
 Group the first three terms. Group the first three terms.
 Factor Factor  to get to get 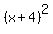 . .
 Combine like terms. Combine like terms.
So after completing the square, 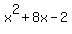 transforms to transforms to  . So . So  . .
So  is equivalent to is equivalent to  . .
Now let's solve 
 Start with the given equation. Start with the given equation.
 Add Add  to both sides. to both sides.
 Combine like terms. Combine like terms.
 Take the square root of both sides. Take the square root of both sides.
 or or  Break up the "plus/minus" to form two equations. Break up the "plus/minus" to form two equations.
 or or  Simplify the square root. Simplify the square root.
 or or  Subtract Subtract  from both sides. from both sides.
--------------------------------------
Answer:
So the solutions are  or or  . .
Notice how we get the same answers. So either method works.
If you need more help, email me at jim_thompson5910@hotmail.com
Also, feel free to check out my tutoring website
Jim
|
|
|
| |