SOLUTION: The line through A(3,1) perpendicular to x - 4y = 8 meets the x-axis at P and the y-axis at Q. Calculate the ratio PA : AQ.

Algebra ->  Coordinate-system -> SOLUTION: The line through A(3,1) perpendicular to x - 4y = 8 meets the x-axis at P and the y-axis at Q. Calculate the ratio PA : AQ.      Log On


   

Question 389043: The line through A(3,1) perpendicular to x - 4y = 8 meets the x-axis at P and the y-axis at Q. Calculate the ratio PA : AQ.
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

Note: the standard slope-intercept form for an equation of a line is y = mx + b  

where m is the slope and b the y-intercept.  

line through A(3,1) perpendicular to x - 4y = 8 OR y = (1/4)x - 2  

Perpendicular lines have slopes that are negative reciprocals of one another

New line y = -4x + b using ordered pair Pt(3,1) to solve for b

         1 = -12 + b     b = 13

         y = -4x + 13   P(13/4,0) and Q(0,13)on this line

Calculate the ratio PA : AQ

PA Distance would be: P(13/4,0)and A(3,1)

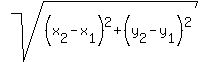
sqrt%28%28x%5B2%5D+-+x%5B1%5D%29%5E2+%2B+%28y%5B2%5D+-+y%5B1%5D%29%5E2%29

PA = sqrt%28%28-.25%29%5E2+%2B+1%5E2%29+=+sqrt%281.0626%29=+1.031++

AQ Distance would be: A(3,1)and Q(0,13)

AQ =  sqrt%28%28-3%29%5E2+%2B+%2812%29%5E2%29+=+sqrt%28153%29+=+12.369+

PA:AQ would be   1.031:12.369