Question 388858: Can someone help me with this problem. I do not understand it I am lost.
Solving a word problem using a quadratic equation with irrational roots
When a ball is thrown, its height in feet h after t seconds is given by the equation
h=vt-16t^2
,
where is the initial upwards velocity in feet per second. If v = 36 feet per second, find all values of t for which h = 19 feet. Do not round any intermediate steps. Round your answer to decimal places.
Thank you very much.
Found 3 solutions by ankor@dixie-net.com, stanbon, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source):
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! When a ball is thrown, its height in feet h
after t seconds is given by the equation
h(t) = vt-16t^2 where "v" is the initial
upwards velocity in feet per second.
-----------------------------------------------
If v = 36 feet per second, find all values of t for which h = 19 feet.
---
Solve: -16t^2+36t = 19
---
-16t^2+37t-19 = 0
---
t = [-37+-sqrt(37^2-4*-16*-19)]/(-32)
---
t = [-37 +-sqrt(153)]/(-32)
---
t = (-37+12.369..]/(-32) or t = (-37-12.369]/(-32)
----
Positive solutions:
t = 0.8723 sec. and t = 1.4045 sec.
Do not round any intermediate steps. Round your answer to decimal places.
==============
Cheers,
Stan H.
==============
Answer by josmiceli(19441)  (Show Source):
You can put this solution on YOUR website! First, try to picture the situation. It
will really help, since you can apply it
to the same type of problem later.
A parabola is the curve that an object
follows when you throw it in the air and
it comes back to the ground.
If the object goes higher than 19 ft, then
it's going to be 19 ft again when it's
on it's way back down.
Look at the equation.
It is a general rule that when the squared term
(that's  ) is negative, then the
parabola has it's peak at the top, and not a dip at
the bottom.
Now I can just apply algebra
Observe that if you have height on the left side, the
right side must also be height, since you can't have
height = speed or height = time, etc.
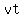 is the contribution to  that is due
to the push of sending the object up.
is a negative contributiuon to
due to gravity wanting to pull the object back down.
given:
Using the quadratic formula:
Note that  , so
and
The answers are:
and
and, since
and
On the way up, object is at height 19 ft in .8455 sec
On the way down, object is at height 19 ft in 1.4045 sec
You can check these
I'll check one answer:
Close enough
|
|
|
