The sum of all 6 sides of a die is 1+2+3+4+5+6 = 21
So the 'Sum of all the Exposed Sides' (which I'll shorten to SES) of a die is
21 minus whichever side is on the bottom, unexposed. So,
The SES of a rolled die is 21-1 = 20 if 1 is on the bottom
The SES of a rolled die is 21-2 = 19 if 2 is on the bottom
The SES of a rolled die is 21-3 = 18 if 3 is on the bottom
The SES of a rolled die is 21-4 = 17 if 4 is on the bottom
The SES of a rolled die is 21-5 = 16 if 5 is on the bottom
The SES of a rolled die is 21-6 = 15 if 6 is on the bottom
In order that the LCM of the SES's of the dice be a multiple of 6, then either:
Case 1. The SES of one of them must have a factor of 6
or else
Case 2. The SES of one of them must have a factor of 3, not 6, and the SES of
the other must have a factor of 2.
Case 1:
Only one of the possible SES's contains a factor of 6, and that is 18, which
occurs when 3 is on the bottom. 18 is divisible by 6. So If 3 is on the bottom
then the SES is 18. Therefore in this case, it doesn't matter what the SES of
the other die is, the LCM will be divisible by 18, and thus divisible by 6. So
all rolls when one of the dice has a 3 on the bottom will have an SES which is
divisible by 6. There are 11 such rolls that have these pairs of sides on the
bottom:
(1,3), (2,3),(3,3),(4,3),(5,3),(6,3),(3,1),(3,2),(3,4),(3,5),(3,6),
Case 2:
If neither SES is 18, then one of the SES's must be 15. That's because 15 is
the only possible SES besides 18 which has a factor of 3, and that occurs when
a 6 is on the bottom. Since an SES of 18 is eliminated in this case, there
are only 2 SES's remaining with a factor of 2, namely, 20 and 16. That's when
a 1 or 5 is on the bottom. There are 4 such rolls that have these pairs of
sides on the bottom.
(1,6), (5,6), (6,1), (6,5)
So there are 11+4 = 15 ways the dice can be rolled and the LCM of the SES's be
divisible by 6.
There are 36 possible rolls, so the desired probability is  which
reduces to
which
reduces to 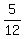 Edwin
Edwin