SOLUTION: Two integers are randomly selected from the set of integers greater than or equal to -6 and less than or equal to 6. The two numbers need not be different. What is the probability

Algebra ->  Probability-and-statistics -> SOLUTION: Two integers are randomly selected from the set of integers greater than or equal to -6 and less than or equal to 6. The two numbers need not be different. What is the probability       Log On


   

Question 388791: Two integers are randomly selected from the set of integers greater than or equal to -6 and less than or equal to 6. The two numbers need not be different. What is the probability that the sum of the two integers is less than their product? Give your answer in as a common fraction in lowest terms?
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

Let the two integers picked be x and y.

First we'll determine the denominator of the desired probability, which
is this set of points (x,y) so that -6%3C=x%3C=6, -6%3C=y%3C=6, 



That is an array of 13x13 or 169 points (x,y).  So the denominator of the
desired probability is 169.  
 
Now let's find the numerator.  We require that (x,y) be such that
 
x + y < xy
 
y - xy < -x
 
y(1-x) < -x
 
Case 1:  1-x > 0
          -x > -1
           x < 1

which of course means -6+%3C=+x+%3C+1
 
Divide both sides of

y(1-x) < -x

by 1-x which is positive and doesn't reverse the <
 
y < %28-x%29%2F%281-x%29
 
y < expr%28%28-x%29%2F%281-x%29%29%2A%28%28-1%29%2F%28-1%29%29
 
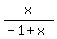y < x%2F%28-1%2Bx%29
 
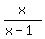y < x%2F%28x-1%29
 
Let's draw the boundary curve y = 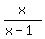x%2F%28x-1%29 for the part involved
in case 1: 



 
 
The solutions for case 1 are the 48 points indicated below the graph above
They form a 7x7 array of points except for (0,0), which is on the graph.
So that makes 49-1 or 48 points, marked above with dots.
 
-------------
 
Case 2:  1-x < 0
          -x < -1
           x > 1
 
which of course means 1+%3C+x+%3C=+6


Divide both sides of

y(1-x) < -x

by 1-x which is negative and thus reverses the <
 
y > %28-x%29%2F%281-x%29
 
y > expr%28%28-x%29%2F%281-x%29%29%2A%28%28-1%29%2F%28-1%29%29
 
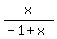y > x%2F%28-1%2Bx%29
 
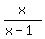y > x%2F%28x-1%29
 
Let's draw the boundary curve y = 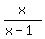x%2F%28x-1%29 for the part involved
in case 2: 

 
 
The solutions for case 2 are the 24 points indicated above the graph above.
They form a 5x5 array of points except for (2,2), which is on the graph.
So that makes 25-1 or 24 points marked above with dots.

That's a total of 48+24 = 72 points. 

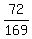So the probability is 72%2F169

To see all 72 points (x,y), let's graph the whole thing. You can see the 48 
points (x,y) under the curve on the left, which came from case 1, and the 24
points (x,y) above the curve on the right, which came from case 2, making 72
in all:



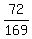Answer: 72%2F169

Edwin