SOLUTION: A box contains 15 yellow, 29 green and 36 red jelly beans. If 10 jelly beans are selected at random, what is the probability that: a) 6 are yellow? b) 6 are yellow and 3

Algebra ->  Probability-and-statistics -> SOLUTION: A box contains 15 yellow, 29 green and 36 red jelly beans. If 10 jelly beans are selected at random, what is the probability that: a) 6 are yellow? b) 6 are yellow and 3      Log On


   

Question 388734: A box contains 15 yellow, 29 green and 36 red jelly beans.
If 10 jelly beans are selected at random, what is the probability that:
a) 6 are yellow?
b) 6 are yellow and 3 are green?
c) At least one is yellow?

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
A box contains 15 yellow, 29 green and 36 red jelly beans.
If 10 jelly beans are selected at random, what is the probability that:
a) 6 are yellow? 
That's (15 yellows, choose 6) AND (29+36=65 non-yellows choose 4)

out of

(15+29+36=80 jelly beans choose 10)

That's 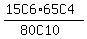 %2815C6%2A65C4%29%2F%2880C10%29 or .0020580634

b) 6 are yellow and 3 are green? 
That's (15 yellows, choose 6) AND (29 greens choose 3) AND (36 reds choose 1)

out of

(15+29+36=80 jelly beans choose 10)

That's  %2815C6%2A29C3%2A36C1%29%2F%2880C10%29 or .0003998668146

c) At least one is yellow? 

This is much easier to do by first finding the probability of the
complement event and then subtracting from 1

The complement event is to choose all non-yellows, that is, 
only greens and reds.

That's 29+36=65 non-yellows, choose 10

out of

(15+29+36=80 jelly beans choose 10)

That's %2865C10%29%2F%2880C10%29 or .10872439

But that's the probability of the complement event.

The probability that you want is 1 - .10872439 or .891275641

Edwin