SOLUTION: Graph f(x) = sin (x − 2π) − 1. Vertical shift =?

For:

f(x) = Asin(Bx + C) + D

Amplitude = |A|
Period =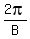 
Phase shift = 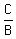, left if  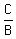is positive, right if  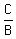is negative

Vertical shift = D, up if D positive, down if D is negative.

---------------------------

For:

Graph f(x) = sin (x − 2π) − 1

f(x) = 1sin(1x + 2p) - 1

A = 1, B = 1, C = -2p, D = -1



Amplitude = |A| = |1| = 1
Period =  =  =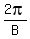 
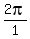Phase shift = 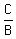 =  = -2, right since  is negative

Vertical shift = D = -1, down since D -1 is negative.

---------------------------

Graph:  Since the phase shift in absolute value equals the period, the
graph of 

f(x) = sin(x − 2π) − 1

is the same as the graph of

f(x) = sin(x) − 1




Edwin