Question 388614: 2. A curve has its equations y=x³-kx²-16x+32
2(a). If the curve crosses the x-axis at A(2,0), find k.
2(b). The point B(p,35) also lies on this curve, find the value of p.
2(c). Calculate the size of the angle between the line AB and the x-axis in the positive direction. Give the answer to the nearest degree.
Found 2 solutions by robertb, lwsshak3:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! (a)  , or 4k = 8, or k = 2. , or 4k = 8, or k = 2.
(b)  , or , or  . The roots of this equation are -3, . The roots of this equation are -3, 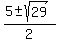 . Therefore the points are . Therefore the points are
(-3, 35), (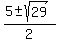 , 35). (Three possibilities!) , 35). (Three possibilities!)
(c) To find the inclination  of the line AB, compute for the slope m of the line AB, and use the formula of the line AB, compute for the slope m of the line AB, and use the formula  , or , or  . .
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! 2a. A(2,0) says that y=0 when x=2.
To solve for k, substitute 2 for x and 0 for y in the given expression, y=x^3-Kx^2-16x+32
0=2^3-2^2K-16(2)+32
4k =8-32+32
4k = 8
k=2
2b. B(p,35) says that when x=p in the given expression, y = 35
To solve for p, substitute p for x, y =35, in the same expression
35 =p^3-(2)p^2-16p +32
0 = p^3-2p^2-16p-3
To solve for p, we can use the possible rational roots theory or, if allowed, use the graphing calculator to determine the roots. According to the rational roots theory, the only possible rational roots are (+ or -1) and (+or-3). If p=-3, the expression becomes 3^3-2(3^2)-16(-3)-3=-27-18+48-3 = 0, and the equation is satisfied. The other rational roots will not satisfy the equation. In addition to -3, p is also equal to two other irrational roots. They can be obtained by dividing the original third degree expression by (x+3) or use synthetic division which will give a second degree equation from which can be determined the two irrational roots.
The second degree equation obtained from division is x^2-5x -1
using the quadradic formula, x = (5 + or - Sqr root of 29)/2
Using the rational root of -3 only, A(2,0) and B(-3,35) the angle between the line AB and the x-axis in the positive direction is determined as follows:
As can be shown on a graph, line AB is the hypotenuse of a right triangle with legs of 35 opposite and 5 adjacent to a supplement of the angle in question.
arc tan (35/5) = 81.87 deg (this is the angle AB makes with the x-axis in the negative direction)
for the positive direction, the angle = 180-81.87 = 98.13 deg
ans: k =2
p=3. or( 5+ or - sqr root of 29)/2 (3 roots, 1 rational and 2 irrational)
Angle line AB makes with x-axis in the positive direction (using (-3,35) point only) = 98.13 deg
|
|
|