SOLUTION: I have to use finite differences to write an equation for the following points: (0,-1) (1,-2) (2,5) (3.38) (4,115) (5,254)

(0,-1) (1,-2) (2,5) (3.38) (4,115) (5,254)

List the second coordinates in a column

 
 -1
 -2
  5
 38
115
254

Subtract each number from the number just below it and write the
difference to the right of that number in a second column. These
numbers are called the first differences.

 -1    3
 -2    7
  5   33
 38   77
115  139 
254

Subtract each number in the second column from the number just below 
it and write the difference to the right of that number in a third 
column.  These numbers are called the second differences.


 -1    3    4
 -2    7   26  
  5   33   44
 38   77   62
115  139 
254

Subtract each number in the third column from the number just below 
it and write the difference to the right of that number in a fourth 
column.  These numbers are called the third differences.


 -1   -1    8   18
 -2    7   26   18
  5   33   44   18
 38   77   62
115  139 
254

We need go no further because we have reached a column in which all
the numbers are the same.  Since this column was the column of 3rd
differences, we assume the formula for the general term is a 3rd degree
polynomial equation:



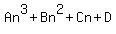That has 4 unknown constants, so we will substitute the first
four first coordinates for n and the second coordinate for 

For n = 0






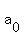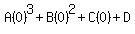
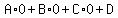
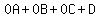
Since we know the value of D as -1, we can now just substitute in




For n = 1







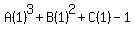
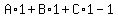
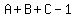
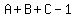
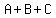For n = 2








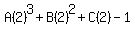
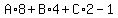
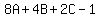
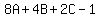
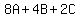
For n = 3







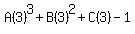
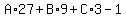
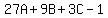
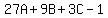
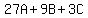So we have the system of 3 equations in 3 variables



Solve that system and get A=3, B=-5, C=1 and we already have D=-1,so



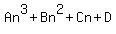becomes:



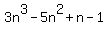Edwin