Question 388194: The number of long distance call between two citties in a certain time period varies jointly as the population of the cities p1 and p2 and inversely as the distance between them. If 60,000 calls are made between two cities 400 miles apart, with populations of 60,000 and 70,000. How many calls are made between cities with population of 90,000 and 95,000 that are two mile apart?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of long distance call between two citties in a certain time period varies jointly as the population of the cities p1 and p2 and inversely as the distance between them. If 60,000 calls are made between two cities 400 miles apart, with populations of 60,000 and 70,000. How many calls are made between cities with population of 90,000 and 95,000 that are two mile apart?
...
long distance calls n
..
distance between cities = d
population p1,p2
...
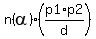
...

...
If 60,000 calls are made between two cities 400 miles apart, with populations of 60,000 and 70,000.
60,000 = k * (60,000*70,000)/400
k= (60,000*400)/(60,000*70,000)
k=1/175
...

...
How many calls are made between cities with population of 90,000 and 95,000.
n= (1/175) * (90,000*95,000/2)
n = 24,428,571 calls
...
m.ananth@hotmail.ca
|
|
|