Question 387883: From a standard 52 card deck what is the probability of 5 card hand having at least one face card?
Answer by gwendolyn(128)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll assume aces are NOT considered face cards. There are Kings, Queens, and Jacks in each of the 4 suits, for a total of 3*4 = 12 face cards.
When trying to determine the probability that there will be at least one in some number of picks, it's easier to determine the probability of the opposite outcome, then subtract it from 1. In this case, let's determine the probability that we get 0 face cards after picking 5 cards, then subtract that probability from 1.
This is a problem of the sort called "sampling without replacement". There is a formula, but it's easier just to walk through the example.
So, what is P(choose no face card on first pick)? It's the number of available non-face cards divided by the number of available cards, or:

When it comes time to choose the second card, what is P(choose no face card on second pick)? It's still the number of available non-face cards divided by the number of available cards. But we know that the first pick must have been a non-face card, so that reduces both the number of remaining non-face cards and the total number of cards by one. So it's:

When it comes time to pick the third card, it's the same story, except the number of available non-face cards and total cards have been reduced by 2:

And so on for each pick until we reach a total of 5 picks. What do we do with each of these individual probabilities? They must ALL be true in order to have the right outcome. In other words you must pick no face card the first time AND no face card the second time AND no face card the third time, etc. That means we can simply multiply those probabilities together.
So, the probability is:

Or,
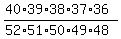 or or

So, this answer is the probability that you will get 0 face cards in five picks. Remember, we need to subtract the probability of this outcome from 1 to get the desired answer (at least one face card in a total of five picks):
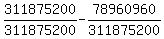 or or
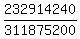
This is the answer as a non-reduced fraction. If an exact answer is desired, you can reduce this fraction. Otherwise, we'll convert it to decimal by doing the division and we come up with 0.7468...
So, in decimal, the probability is 74.68...% (or about 75%) that at least one card out of five picks will be a face card.
|
|
|