Question 387694: i have to face exam next monday.before it toget confidence i ant to know this ones solution.plz any tuter give me answer soon as possible
The weights, in grams, of a consignment of apples are normally distributed with mean μ and
standard deviation 4. A sample of size 25 is taken and the statistics R and T are calculated as
follows:
R = X25 – X1 and T = X1 + X2 + ….. + X25.
Find the distributions of R and T.
2. A large bag contains counters. Sixty per cent of the counters have the number 0 on them and
40% have the number 1.
(a) Find the mean μ and the variance σ2 for this population of counters.
A random sample of size 3 is taken from this population.
(b) List all possible samples.
(c) Find the sampling distribution for the mean X =
3
1 2 3 X X X
where X1, X2 and X3 are
the three variables representing samples 1, 2 and 3.
(d) Hence find E ( X ) and Var( X ).Find the sampling distribution for the mode M.
(f) Hence find E (M) and Var(M).
4. A machine operator checks a random sample of 20 bottles from a production line in order to
estimate the mean volume of bottles (in cm3) from this production run. The 20 values can be
summarized as Σx = 1300 and Σx2 = 84685.
(a) Use this sample to find unbiased estimates of μ and σ2.
(b) A supervisor knows from experience that the standard deviation of volumes on this
process, σ, should be 3 cm3 and he wishes to have an estimate of μ that has a standard
error of less than 0.5 cm3.
What size sample will he need to achieve this?
(c) The supervisor takes a further sample of size 16 and finds Σx = 1060.
Combine the two samples to obtain a revised estimate of μ.
5. An electrical company repairs very large numbers of television sets and wishers to estimate the
mean time taken to repair a particular fault.
It is known from previous research that the standard deviation of the time taken to repair this
particular fault is 2.5 minutes.
The manager wishes to ensure that the probability that the estimate differs from the true mean by
less than 30 seconds is 0.95. Find how large a sample is required.
7. A manufacturer of self-assembly furniture required bolts of two lengths, 5 cm and 10 cm, in the
ratio 2: 1.
(a) Find the mean μ and the variance σ2 for the lengths of bolts in this population.
A random sample of three bolts is selected from a large box containing bolts in the
required ratio.
(b) List all possible samples.
(c) Find the sampling distribution for the mean
X
(d) Hence find E(
X ) and Var (
X ).
(e) Find the sampling distribution for the mode M.
(f) Hence find E(M) and Var (M).
(g) Find the bias when M is used as an estimator of the population mode.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! For now I'll just do 2 and 3(?).
A large bag contains counters. Sixty per cent of the counters have the number 0 on them and
40% have the number 1.
(a) Find the mean μ and the variance σ2 for this population of counters.
A random sample of size 3 is taken from this population.
(b) List all possible samples.
(c) Find the sampling distribution for the mean X =
3
1 2 3 X X X
where X1, X2 and X3 are
the three variables representing samples 1, 2 and 3.
(d) Hence find E ( X ) and Var( X ).Find the sampling distribution for the mode M.
(f) Hence find E (M) and Var(M).
---------------------------------------------------------------------------------
(a) It is binomially distributed, with the following distribution:
X | 0 1
-------------------
p(X ) | 0.60 0.40
Then 

(b)Sample space = {000,001,010,011,100,101,110,111}.
(c) sampling distribution of the mean X`
X` ---> 0 1/3 2/3 1
p(X`) ---> 27/125 54/125 36/125 8/125
(d) Then  (X`) = (X`) =  , and , and
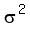 (X`) = (X`) =  . .
(e) Sampling distribution of the mode:
M ---> 0 1
p(M) ---> 81/125 44/125
The mode is 0 if there are 3 or 2 0's, and 1 is the mode if there are 3 or 2 1's.
(f)  , while , while  . .
|
|
|