SOLUTION: Prove lines containing the altitudes of any triangle are concurrent

Algebra ->  Geometry-proofs -> SOLUTION: Prove lines containing the altitudes of any triangle are concurrent      Log On


   

Question 387008: Prove lines containing the altitudes of any triangle are concurrent
Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
Suppose triangle ABC has altitudes AD, BE, CF. Without loss of generality, let AD and BE meet at H. We want to prove that H lies on CF.

On the contrary, suppose H is not on CF. Then, by Ceva's theorem,

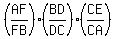%28AF%2FFB%29%28BD%2FDC%29%28CE%2FCA%29 is not equal to 1 since the three segments are not concurrent.

We can show that CE%2FCD+=+BE%2FAD, AF%2FAE+=+FC%2FBE, and BD%2FBF+=+AD%2FFC using similarities within the right triangles ADC, AFC, etc. Multiplying all three equations,

%28CE%2FCD%29%28AF%2FAE%29%28BD%2FBF%29+=+%28BE%2FAD%29%28FC%2FBE%29%28AD%2FFC%29 The right side of the equation cancels to 1, so

%28CE%2FCD%29%28AF%2FAE%29%28BD%2FBF%29+=+1

However, the left side of the equation is equivalent to our first equation, so 1 is equal to some quantity other than 1, contradiction. Therefore the three altitudes must be concurrent.