SOLUTION: A card is selected from a deck of 52 playing cards. Find the probability of selecting · an even number ten or less given the card is a not a diamond. · an Ace

Algebra ->  Probability-and-statistics -> SOLUTION: A card is selected from a deck of 52 playing cards. Find the probability of selecting · an even number ten or less given the card is a not a diamond. · an Ace      Log On


   

Question 385489: A card is selected from a deck of 52 playing cards. Find the probability of selecting

· an even number ten or less given the card is a not a diamond.
· an Ace, given that the card is black.
· a spade given the card is red.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
Here is a standard deck of 52 cards:

 
A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 
A♦   2♦   3♦   4♦   5♦   6♦   7♦   8♦  9♦  10♦  J♦  Q♦  K♦
A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣ 

Probability of
an even number ten or less given the card is a not a diamond.
 

Since we are given that it is not a diamond, we can take out all the diamonds,
and this is what we have left:

A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 

A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣

There are 39 of them.  Now I will underline all the cards that are even number
ten or less: 


A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 

A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣

Count them and you'll see there are 15 underlined cards, so the
probability is 15 out of 39 or 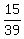15%2F39 which reduces to 5%2F13

-----------------------------------------------------------------------

As before we start with a standard deck of 52 cards:


 
A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 
A♦   2♦   3♦   4♦   5♦   6♦   7♦   8♦  9♦  10♦  J♦  Q♦  K♦
A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣ 

Probability of
an Ace, given that the card is black.

Since we are given that the card is black, we will take away all the red ones,
leaving only what is given, the black cards:
 
A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣ 
 
There are only 26 cards. And only 2 are aces.  So the probability is 2 out
of 26 or 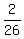2%2F26 wich reduces to 1%2F13

---------------------------------------------------------

As before we start with a standard deck of 52 cards:


 
A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 
A♦   2♦   3♦   4♦   5♦   6♦   7♦   8♦  9♦  10♦  J♦  Q♦  K♦
A♠   2♠   3♠   4♠   5♠   6♠   7♠   8♠  9♠  10♠  J♠  Q♠  K♠  
A♣   2♣   3♣   4♣   5♣   6♣   7♣   8♣  9♣  10♣  J♣  Q♣  K♣

Probability of
a spade given the card is red.

Since we are given that the card is red, we take away all the black cards,
leaving all the red cards:


 
A♥   2♥   3♥   4♥   5♥   6♥   7♥   8♥  9♥  10♥  J♥  Q♥  K♥ 
A♦   2♦   3♦   4♦   5♦   6♦   7♦   8♦  9♦  10♦  J♦  Q♦  K♦

There are only 26 cards left.

But there are no spades left.  So the probability is 0 out of 26 or 0%2F26
or 0. 

Edwin