Question 384724: Solve:
a) log(base4)(2) + log(base9)(2x+5) = log(base 8)(64)
b) 9^y + 5(3^y - 10) = 0
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! a. 
We can start by figuring out two of the three logarithms. The most obvious one is the last one. What power of 8 is 64? Answer: 2. So  . And what power of 4 is 2? Answer: 1/2 (Not because 2 is 1/2 of 4 but because 2 is the square root of 4 and 1/2 as an exponent means square root. So 
We want the logarithm isolated so we'll subtract 1/2 from each side:
With the equation in this form the next step is to rewrite the equation in exponential form. In general  is equivalent to  . Using this pattern on your equation we get:
If you have trouble simplifying negative and/or fractional exponents it can be helpful to factor the exponent in a special way:- If the exponent is negative, factor out -1.
- If the exponent is a fraction, factor out the numerator (leaving 1/denominator).
Factoring your exponent as described above we get:
Looking at the exponent in factored form...- The 3 tells us we will be cubing.
- The 1/2 tells us we will be finding a square root.
And, since multiplication is Commutative, we do do these operations in any order we choose! So we want to cube 9 and then find a square root? Or find the square root of 9 and then cube? Since the square root of 9 is easy I'll choose to start with that. (If you cube first, the answer works out the same!).
Substituting this value in our equation now looks like:
2x + 5 = 27
This is a simple equation to solve. Subtract 5 from each side:
2x = 22
Divide both sides by 2:
x = 11
When solving logarithmic equations you must check your answers. You must ensure that your answers make all arguments (and bases) of logarithms positive. If a "solution" makes an argument (or base) zero or negative you must reject that "solution". And this can happen even if no mistakes were made.
When checking, always use the original equation:
Checking x = 11:
We can already see that all bases and arguments will be positive when x = 11. So we will not have to reject this solution. The rest of the check will tell us if we made a mistake:
Since we already found that  , so  . This gives us:
2 = 2 Check!
So the solution x = 11 is correct.
b. 
First we'll simplify:
The key to this problem is recognizing that - if we replace 9 with
 the equation will be in quadratic form.
Substituting for 9:
The rule for exponents when raising a power to a power is to multiply the exponents. This gives us:
This equation is in quadratic form for 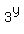 . IOW, the exponent on the first term is twice the exponent on the middle term. So we can use quadratic methods to solve this. (If you have trouble seeing this as being "quadratic form, it can help to use a temporary variable:
Let q =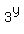
Then 
Substituting this into our equation we get:
This is clearly a quadratic equation. One side is already zero and the other side factors fairly easily:
(q + 10)(q - 5) = 0
From the Zero Product Property we know that this (or any) product can be zero only if one (or more) factors is zero. So:
q + 10 = 0 or q - 5 = 0
Solving these we get:
q = -10 or q = 5
We have solved for q. But we want to solve for y. So we substitute back in for the temporary variable:
 or 
Since 3 to any power can never be negative, there will be no solutions to the first equation. We will however get a solution from the second equation.
To solve the second equation we will need logarithms. We can use any base of logarithm but- if we pick base 3 logarithms we will get the simplest exact expression for the solution (because 3 is the base of the exponent).
- if we pick base 10 or base e (aka ln) logarithms we will be able to find a decimal approximation more easily.
I'm going to use base 3 logarithms:
Next we can use a property of logarithms,  , to move the exponent of the argument out in front:
By definition  . (This is why base 3 logarithms give us the simplest answer.) Replacing this log with a 1 ans simplifying we get:
This is an exact expression for the solution.
If you decide later to find a decimal approximation, you can use the base conversion formula,  , to convert 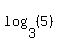 to base 10 or base e logarithms. Then you can use your calculator.
After you have done a few of these quadratic form equations, you will no longer need a temporary variable. You will see how to go from:
to factoring:
to the Zero Product Property:
 or 
etc.
|
|
|
