SOLUTION: 1) The length of a rectangular garden is 2 yd greater than the width. The area is 80 yd2. Find the length and width. I also have a next problem that an a little lost on: 2) G

Hi,         

1) Let x and (x+ 2yd) represent the width and length respectively

  x(x+2) = 80 yd^2

  x^2 + 2x  - 80 = 0

  factoring

(x+10)(x-8) = 0 Note:SUM of the inner product(10*x) and the outer product(-8x) = 2x

(x+10)=0

  x = -10  Tossing out negative solution

(x-8) = 0

  x = 8yd , the width, the length 10yd     (8yd + 2yd)



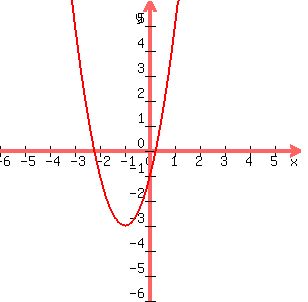
2)find the coordinates of the vertex:

the vertex form of a parabola,  where(h,k) is the vertex

y=2x^2+4x-1  Completing the square

 y = 2[(x +1)^2 -1] - 1

 y = 2(x+1)^2 - 2 - 1

 y = 2(x+1)^2 - 3

  Vertex Pt(-1,-3)