Question 384084: Carrel Brady invests $500 in an account that earns 4.28% compounded continuously and $1000 in an
account that earns 5.20% compounded quarterly. Use graphical approximation methods to determine how long it
will take for his total investment in the two accounts to grow to $3000.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation for quarterly compounding would be:
y = 1000 * (1.013)^x where x is the number of quarterly compounding periods.
1000 is the initial investment
.013 is the annual interest rate of .052 divided by 4 to get a quarterly interest rate.
x is the number of quarterly compounding periods
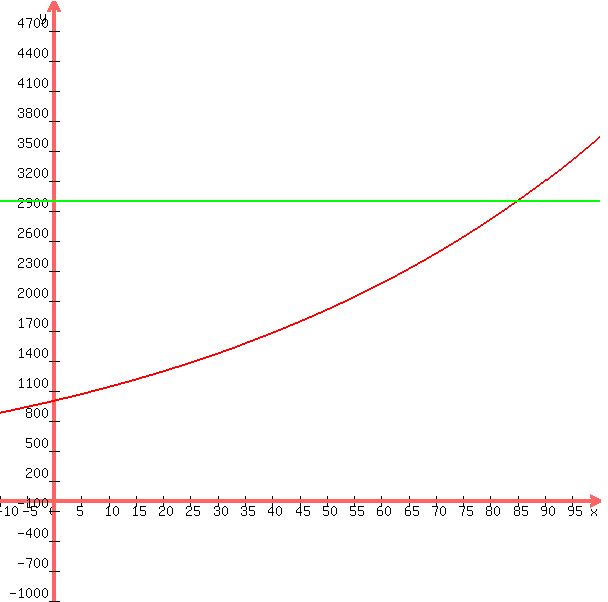
The graph of the quarterly compounding equation is shown below:
Equation for continuous compounding would be:
y = 500 * e^(.048*x) where x is the number of years.
500 is the initial investment
.048 is the annual growth rate
x is the number of years
e is the scientific constant of 2.718281828...
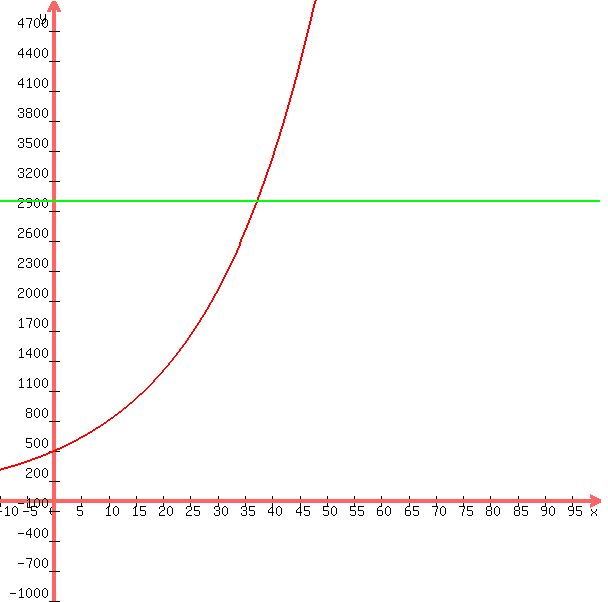
The graph of the continuous compounding equation is shown below:
With quarterly compounding, the value of x represents the number of quarterly compounding periods (4 compounding periods per year). This means that the number of years is equal to the number of compounding periods divided by 4.
From the graph, it appears that the initial value of 1000 reaches 3000 in approximately 85 quarters which is equivalent to 21.25 years.
With continuous compounding, the value of x represents the number of years.
From the graph, it appears that the initial value of 500 reaches 3000 in approximately 37 or 38 years.
We can solve for this algebraically.
With quarterly compounding, the formula would become:
3000 = 500 * (1.013)^x
We use logs to solve this.
The answer is x = 85.05676124 which is pretty close to x = 85.
Don't forget that this is quarters, not years. To get years, you need to divide by 4.
With continuous compounding, the formula would become:
3000 = 500 * e^(.048*x)
We use logs to solve this as well.
The answer is x = 37.32832228
If you need to know how I solved this using logs, let me know and I'll send you the details of the solution.
Otherwise, I'm just showing you that the approximate values shown by the graph are close to the actual values that were calculated algebraically.
The key to graphing the quarterly compounding formula is that x represents the number of quarters, not the number of years.
|
|
|