Question 383881: After discontinuing all advertising for a certain product (in 1995), the manufacturer of the product found that the sales began to drop according to the model,
S= 500,000/(1+0.6^(kt)) 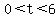
Where S= represents the number of units sold
t= the calendar year with t=0 being 1995
k= rate of decline
*that S part above is a fraction where the 500,000 is the numerator and the 1+0.6kt is the denominator. The kt should be elevated (like an exponent), but I have no idea how to do that on this silly computer. Also the value for t is less than or equal to (again, my computer illiteracy won't let me figure out how to type that either.)
a) Find k if the company sold 300,000 units in 1997...that is let S= 300,000
b) Now, using the rate (k) that you found above, what were the sales in 2000?
c)What did the company learn about advertising for the product?
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
S= 500,000/(1+0.6^(kt)) 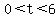
3*10^5=5*10^5/(1+0.6^(2k)
1+.6^2k/5*10^5=1/3*10^5
1+6^2k=5*10^5/3*10^5
1+6^2k=5/3
6^2k=2/3
log[6]6^2k=log[6](2/3)
2k=-.2263
.
k=-.1131
.
b)
S=5*10^5/1+0.6^(-.1131*5)
=$214,140.
.
Ed
|
|
|