|
Question 383763: find the domain of the function f (x) = square root of 12 − 3x^2
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The domain is the set of values of x that can be substituted into a
functional equation.
Negative numbers cannot be permitted under a square root radical, because you
can't multiply a negative by itself, which is a negative) and get a negative,
because you'll always get a positive,
  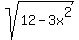 So what is under that radical cannot be negative. So we cannot substitute any
number for x and get an answer that will make
So what is under that radical cannot be negative. So we cannot substitute any
number for x and get an answer that will make  a negative number.
So we set it a negative number.
So we set it  zero, so it won't be negative. zero, so it won't be negative.
   We can divide through both sides by 3 without reversing the inequality because
we are dividing through by a positive number, not by a negative number.
(If we had divided both sides by a negative number we would
have had to reverse the symbol of imequality).
We can divide through both sides by 3 without reversing the inequality because
we are dividing through by a positive number, not by a negative number.
(If we had divided both sides by a negative number we would
have had to reverse the symbol of imequality).
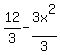  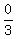
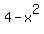   Now factor:
Now factor:
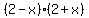   The critical values are found by setting the left side equal to zero.
2-x=0 has solution x=2
2+x=0 has solution x=-2
Therefore these are the critical numbers. We mark them on a number
line with open circles "o" (but we may close them later).
-------------o---------------o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
We pick a test value left of -2, say -3 since it's the easiest. We substitute
-3 in
The critical values are found by setting the left side equal to zero.
2-x=0 has solution x=2
2+x=0 has solution x=-2
Therefore these are the critical numbers. We mark them on a number
line with open circles "o" (but we may close them later).
-------------o---------------o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
We pick a test value left of -2, say -3 since it's the easiest. We substitute
-3 in
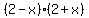   to see if it's true or false.
to see if it's true or false.
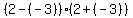  
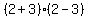  
  
   That's false so we do not shade that part of the number line, so we still just
have this:
-------------o---------------o---------
-5 -4 -3 -2 -1 0 1 2 3 4
Next we pick a test value between -2 and 2, say 0 since it's the easiest. We
substitute 0 in
That's false so we do not shade that part of the number line, so we still just
have this:
-------------o---------------o---------
-5 -4 -3 -2 -1 0 1 2 3 4
Next we pick a test value between -2 and 2, say 0 since it's the easiest. We
substitute 0 in
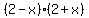   to see if it's true or false.
to see if it's true or false.
  
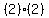  
   That's true so we shade that part of the number line, and now we have
this:
-------------o===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Next we pick a test value right of +2, say +3 since it's the easiest.
We substitute +3 in
That's true so we shade that part of the number line, and now we have
this:
-------------o===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Next we pick a test value right of +2, say +3 since it's the easiest.
We substitute +3 in
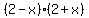   to see if it's true or false.
to see if it's true or false.
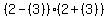  
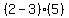  
  
   That's false so we do not shade that part of the number line,
so we still just have this:
-------------o===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Next we test the critical points themselves, -2 and +2
Testing -2
That's false so we do not shade that part of the number line,
so we still just have this:
-------------o===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Next we test the critical points themselves, -2 and +2
Testing -2
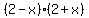  
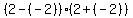  
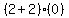  
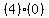  
   This is true so we darken the circle at -2
-------------@===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Testing +2
This is true so we darken the circle at -2
-------------@===============o---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
Testing +2
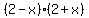  
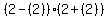  
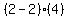  
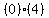  
   This is true too so we darken the circle at +2
-------------@===============@---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
In interval notation this is [-2, 2]
Edwin
This is true too so we darken the circle at +2
-------------@===============@---------
-5 -4 -3 -2 -1 0 +1 +2 +3 +4
In interval notation this is [-2, 2]
Edwin
|
|
|
| |