|
Question 382728: Please help me with this: A bridge is to be built in the shape of a parabolic arch and is to have a span of 100 feet. The height of the arch at a distance of 40 ft from the center is to be 10 ft. Find the height of the arch at its center.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bridge is to be built in the shape of a parabolic arch and is to have a span of 100 feet.
The height of the arch at a distance of 40 ft from the center is to be 10 ft.
Find the height of the arch at its center.
;
Find the equation using the form ax^2 + bx = y
:
From the information given, we can find two x,y coordinates
x = the width of the bridge, y = height of the bridge at x
x=100, y=0
and it says,"height of the arch at a distance of 40 ft from the center is to be 10 ft"
The center of the bridge = 50 ft, 40 ft to left of center: x=10
x=10, y = 10
and
x=100, y=0
100^2a + 100b = 0
10000a + 100b = 0
and
x=10, y=10
10^2a + 10b = 10
100a + 10b = 10
Multiply the above equation by 10 subtract from the 1st equation
10000a + 100b = 0
1000a + 100b = 100
-----------------------subtraction eliminates b, find a
9000a = -100
a = 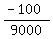
a = -.011
:
Find b using 100a + 10b = 10
100(-.011) + 10b = 10
-1.11 + 10b = 10
10b = 10 + 1.11
b = 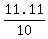
b = 1.111
:
The equation: y = -.011x^2 + 1.11x, graph would look like this

You can see that 40' either side of the center (50') the arch is 10' high
:
What is the height at the center? Substitute 50' for x in the equation, find y
y = -.011(50^2) + 1.11(50)
y = -27.5 + 55.5
y = 28 ft, which is about right on the graph
|
|
|
| |