Question 382349: 1) solve the equation 4^x-3*2^x-4=0
2)solve the equation log2(x-4)-log2(x+3)=8
Found 2 solutions by Fombitz, jsmallt9:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) solve the equation 
The keys to one way to solve this is know:- that
 , and , and - how to recognize and solve equations that are in quadratic form.
We'll start by replacing the 4 of  with with 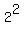 : :

By the rules of exponents for powers of a power, we multiply the exponents:

Since the exponent of the first term is twice the exponent in the middle term, this equation is in "quadratic form" for 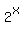 . If you have trouble seeing this, we can use a temporary variable: . If you have trouble seeing this, we can use a temporary variable:
Let q = 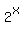 . Then . Then  . Substituting these into the equation we get: . Substituting these into the equation we get:

This is clearly a quadratic equation. To solve it we want one side to be zero (which we already have) and then factor (or use the Quadratic Formula). This factors easily:
(q-4)(q+1) = 0
From the Zero Product Property we know that this (or any) product is zero only if one (or more) of the factors is zero. So:
q-4 = 0 or q+1 = 0
Solving these we get
q = 4 or q = -1
Of course we are not interested in solutions for q, We want solutions for x. So we substitute back in for q. (After all, q was supposed to be temporary.) Now we have:
 or or 
There is no power of 2 that will result in a negative so we will not get a solution from the second equation. And the solution to the first equation is obvious, I hope:
x = 2
2)solve the equation 
Solving equations like this, where the variable is in the argument of a logarithm, one usually start by transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
With the "non-log" term of 8, your equation can more easily transformed into the first form. So somehow we need to find a way to combine the two logarithms into one. Fortunately there is a property of logarithms,  , which allows us to do exactly that! , which allows us to do exactly that!

This equation is now in the first form. With the first form the next step is to rewrite the equation in exponential form. In general  is equivalent to is equivalent to  . Using this pattern on our equation we get: . Using this pattern on our equation we get:

Since  this becomes: this becomes:
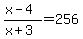
Now we solve this equation. We can start by multiplying both sides by (x+3) (to eliminate the fraction):
x-4 = 256(x+3)
which simplifies to:
x-4 = 256x + 768
Subtracting x we get:
-4 = 255x + 768
Subtracting 768 we get:
-772 = 255x
And last of all, divide by 255:

With logarithmic equations like this one, you must check your answers. It is not just a good idea. You must ensure that no argument of any logarithm becomes negative or zero. And when checking, always use the original equation:

Checking x = -28/9:

If we can't see it already, it will become obvious soon that both arguments are going to be negative with x = -772/255. Since we cannot allow negative arguments to logarithms we must reject this solution. (Note: If even one argument was negative (or zero), we would still have to reject the solution.)
The fact that we are rejecting -772/255 does not mean we made a mistake somewhere! This kind of thing can happen any time you are solving equations like this. This is why it is important to check.
Since we rejected the only "solution" we were able to find, there is no solution to your equation.
|
|
|