Question 382210: Solve the following logarithmic equation. if there is no solution, state No Solution (Round your to 4 decimal places)
ln(x-2)+ln(x)=0
Found 2 solutions by stanbon, jsmallt9:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Solve the following logarithmic equation. if there is no solution, state No Solution (Round your to 4 decimal places)
ln(x-2)+ln(x)=0
---
ln[(x-2)(x)] = 0
---
x(x-2) = 10^0 = 1
----
x^2-2x-1 = 0
----
x = [2 +- sqrt(4-4*1*-1)]/2
----
x = [2 +- sqrt(8)]/2
----
x = [2 +- 2sqrt(2)]/2
----
x = [1 +- sqrt(2)]/2
=========================
Only acceptable solution:
x = (1+sqrt(2))/2 = 1.2071
=========================
Cheers,
Stan H.
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! ln(x-2) + ln(x) = 0
To solve equations like this, where the variable is in the argument (or base) of a logarithm one usually starts by transforming the equation into one of the following forms:
log(expression) = other-expression
or
log(expression) = log(other-expression)
With the "non-log" term of 0, it will be easier to transform your equation into the first form. We just have to combine the two logarithms into one somehow. Fortunately there is a property of logarithms,  , that will allow us to do just that. Using this on your equation we get:
ln((x-2)*(x)) = 0
This is the first form. With the first form the next step is to rewrite the equation in exponential form. In general,  is equivalent to  . Using this pattern on your equation we get:
Since  and  this becomes:
This is a quadratic equation so we want one side to be zero. Subtracting 1 from each side we get:
And then we factor (or use the Quadratic Formula). This does not factor easily so we will use the Quadratic Formula:
which simplifies as follows:
In long form this is:
 or 
With logarithmic equations like yours, it is important, not just a good idea to check your answers. You must ensure that your solution(s) make all arguments (and bases) of logarithms positive. Any "solution" that makes an argument (or base) negative (or zero) must be rejected!
When checking, always use the original equation:
ln(x-2) + ln(x) = 0
Checking :
Since 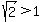 we can see that the arguments of both logarithms will be positive. The rest of the check will only tell us if we made a mistake. You are welcome to finish the check.
Checking :
We can see that both arguments are negative here. So we must reject this "solution". This does not mean we made a mistake! This can always happen with these equations. This is why we must check. (Note: If only one argument had been negative (or zero), then we would still reject this "solution".)
So the only solution to your equation is:
This is an exact expression for the solution. Since the instructions say "Round to 4 decimal places" then it is clear that a decimal approximation is desired. Get out your calculator, find the square root of 2, add 1 to it and then round your answer as described.
|
|
|
