First a little background, which you may already be familiar with.
[Since no complex integer can be said to be "greater" than another, nor
the "greatest" in a set, one might think it should be meaningless to speak of
a "greatest" common divisor. However not all common divisors are divisible
by all other common divisors. For instance ±1, ±i and 1+i are all common
divisors of 2+2i and 3+3i. However ±1, ±i are not divisible by 1+i, athough
1+i is divisble by them. We reserve the term "greatest" for a common divisor
that is divisible by ALL common divisors. "Greatest" is still a misnomer,
since none are really "greater" than any of the others, but we still use the
term "GCD" to refer to any common divisor that is divisible by ALL common
divisors.]
Since there are 4 unit complex integers, ±1, ±i, there are 4 associate
GCD's of any two complex integers. That is, if a+bi is a GCD of p+qi
and r+si then all four of these are also GCDs of p+qi and r+si.
1(a+bi) = a+bi
-1(a+bi) = -a-bi
i(a+bi) = ai+bi² = ai+b(-1) = ai-b = -b+ai
-i(a+bi) = -ai-bi² = -ai-b(-1) = -ai+b = b-ai
To use the Euclidean algorithm, we begin by dividing one by the other until
we get a remainder of 0.
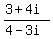
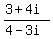
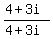
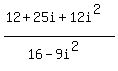
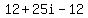
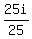
What do you know! We got a complex integer on the first division.
The remainder is therefore 0, since we got a complex integer, in fact,
the complex unit i, so the set of four associate GCDs are 1,-1, i, and -i
times the last divisor used, which was 4-3i, and they are, as we saw above:
{4-3i, -4+3i, 3+4i, -3-4i}
Those are the answers.
[Notice that there are other common divisors of 3+4i and 4-3i, and not
just ±1 and ±i, either. For 2+i, -2-i, 1-2i, and -1+2i are also common
divisors of 3+4i and 4-3i as well. However, none of these are divisible by
any of the four associate GCDs, so they are not GCDs. However the four
associate GCDs are divisible by them.]
Edwin
