Question 380915: Write the expression log2(6x/y) as a sum and/ or difference of logarithms
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! log(2,6x/y) is equal to the log of 6x/y to the base of 2.
it means the same as what you wrote as log2(6x/y).
the notation, however, is more in line with the way the algebra.com formula generators work.
using the algebra.com formula generator, log(2,6x/y) will show up as 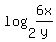
All you do is put 3 { in front of it and 3 } behind it.
in general, log(x/y) = log(x) - log(y)
your equation becomes:
log(2,6x/y) = log(2,6x) - log(2,y)
in general, log (x*y) = log(x) + log(y)
your equation becomes:
log(2,6x/y) = log(2,6) + log(2,x) - log(y)
the concept is the same regardless of the base.
if the base were 10, then it would be shown as:
log(10,6x/y) = log(10,6) + log(10,x) - log(10,y)
to show you how it works, we'll use log to the base 10 because your calculator can handle that.
also, log(10,x) is normally shown as log(x).
the base of 10 is implied.
let's take log(6*15/30)
this should be translated to log(6) + log(15) - log(30) which is the same treatment we provided above.
using our calculator, we get log(6*15/30) = log(3) = .477121255
using our calculator again, we get log(6) + log(15) - log(30) = :
.77815125 + 1.176091259 - 1.477121255 = .477121255
we get the same answer, as we should.
same concepts works with any base, so the answer to your question is:
log(2,6x/y) = log(2,6) + log(2,x) - log(2,y).
|
|
|