Question 379865: Factor the polynomial f(x) then solve the equation f(x)=0
f(x)=x^4-4x^3-7x^2+22x+24
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
The Greatest Common Factor is 1 (which we usually don't bother factoring out. There are four terms and this is too many to factor using patterns or trinomial factoring. So we are left with factoring by grouping and factoring by trial and error of the possible rational roots. I don't see how factoring by grouping will work so we are left with the rational roots.
The possible rational roots of a polynomial are all the ratios/fractions, positive and negative, which can be formed using a factor of the constant term (at the end) in the numerator and a factor of the leading coefficient (in front of the term with the highest exponent). So the possible rational roots of your polynomial are: 1/1, -1/1, 2/1, -2/1, 3/1, -3/1, 4/1, -4/1, 6/1, -6/1, 8/1, -8/1, 12/1, -12/1, 24/1, -24/1. (Since all the denominators are 1's these are all whole numbers.)
This is quite a long list and this is a trial and error process so it can take a while to find some, if any, that work. To save time, I am only going to show ones that work. The easiest way to check these roots is, IMHO, synthetic division:
-1 | 1 -4 -7 22 -24
---- -1 5 2 -24
-------------------
1 -5 -2 24 0
The zero in the lower right corner is the remainder. A remainder of zero means that (x-(-1)) or (x+1) divides evenly into the polynomial. And if (x+1) divides evenly then it is a factor of the polynomial. (Note: A non-zero remainder means the it did not divide evenly, a factor has not been found and you have to try another possible rational root.) Not only have we found that (x+1) a factor but the rest of the bottom line, "1 -5 -2 24" tells us that the other factor is: 
We need to keep factoring and we are still "stuck" with the rational roots as the only way to do so. At this point however, we are factoring not the original polynomial but the factor . Again I will just show a rational root that works:
-2 | 1 -5 -2 24
---- -2 14 -24
--------------
1 -7 12 0
So (x-(-2)) or (x+2) is a factor and the other factor is 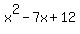 . The remaining factor is a quadratic trinomial which factors easily into (x-3)(x-4). (Note: These last two factors mean that, back when we were trying the rational roots, 3 and 4 would also have worked. IOW, -1 and -2 were not the only rational roots that work.)
We have now factored the polynomial completely.
Now that we have factored f(x), the Zero Product Property tells us that the solutions to f(x) = 0 (aka roots) are the values of x that make a factor zero. So:
x+1 = 0 or x+2 = 0 or x-3 = 0 or x-4 = 0
Solving each of these for x we get:
x = -1 or x = -2 or x = 3 or x = 4
|
|
|
