Question 379863: I cannot understand the question if 3^4x=6^1-x show that x=(log 6)/(log 486).
Is the 3^4x=6^1-x relavent in this question?
if so, then do you have to solve 3^4x=6^1-x first, then solve x=(log 6)/(log 486)?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
This is the equation to solve. You are supposed to show how/why 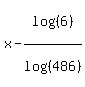 is a solution to the equation.
To solve equations where the variable in in exponents like this, you use logarithms. (I'll explain why in a little bit.) Usually you can choose a logarithm of any base you want to choose. But since the given answer is in base 10 logarithms, I will use them:
Next we use a property of logarithms,  , to "move" the exponents of the arguments out in front of the logarithms. This property of logarithms is the very reason we use logarithms on equations like this. The variable is in the exponent(s). And by using this property to move the exponents out in front, we can then use "regular" Algebra to solve for the variable. Using this property on the two logarithms in your equation we get:
Next we can use the Distributive Property to multiply on the right side:
(4x)*log(3) = log(6) - x*log(6)
Next we gather the x terms on one side of the equation and the other ("non-x") terms on the other side (by adding x*log(6) to each side):
(4x)*log(3) + x*log(6) = log(6)
Next we factor out x:
x(4*log(3) + log(6)) = log(6)
Then we divide both sides by (4*log(3) + log(6)):
We have solved for x. Even though this does not match the answer you were given it is correct. To finish your problem we need to show that what we got above is equal to the answer you were given.
The numerators match exactly. But the denominator is different. Somehow we need to show that our denominator is equal to the one you were given. To do this we will use the same property that we used earlier, in reverse, to move the 4 from in front into the argument as the exponent. (Most properties in Math can be used in both directions.):
 so this becomes:
Next we will use another property of logarithms,  , to combine the two logarithms into one. This property requires that:- The bases of the logarithms are the same.
- There is a plus sign between the two logarithms.
- The coefficients of the logarithms are 1's. (This is why we had to move the 4 from in front in the previous step.)
The two logarithms in the denominator meet all three requirements so we can use it:
And, believe it or not, 81*6 = 486! So this simplifies to:
This and the answer we got earlier () are both exact expressions for the solution to the equation. (If you want a decimal approximation of the solution, you can get out your calculator, find the two logarithms and then divide them.)
|
|
|
