Question 379858: Having trouble with a logarithm! I am okay with logarithms, but this one throws in a square root so I am lost as to what to do with it.
log base-2 (log base-b (sqrt b)) , where b > 0.
I just had a thought.. do I need to turn sqrt b into b^(1/2)?
Any help would be appreciated, thanks! :)
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 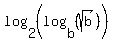
You are correct. start by rewriting 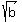 as as 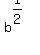 : :
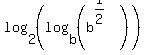
Next, on the inner logarithm, we can use a property of logarithms,  , to "move" the exponent of the argument out in front of the logarithm: , to "move" the exponent of the argument out in front of the logarithm:

By definition,  so this becomes: so this becomes:

The quick way to finish requires that we understand what this expression represents. It represents the exponent for 2 that results in 1/2. If you also understand exponents, you will know that the answer is: -1!
The long way is to use another property of logarithms,  , to split the numerator and denominator into separate logarithms: , to split the numerator and denominator into separate logarithms:

The logarithm of 1, regardless of the base, is zero (because any number to the zero power is 1). And by definition  . So now we have: . So now we have:
0 - 1
which equals
-1
|
|
|